ALevel數學經典知識點！揭秘奇妙的“楊輝三角”與概率論背後的關係！

楊輝三角

早在北宋時期，我國數學家賈憲就發現了任意的高次方展開係數符合某種三角形的運算規律。200年後，南宋數學家楊輝在其著作《詳解九章算術》中，詳細解釋了這種運算規律，並給出了一種數表，也叫做楊輝三角，300多年後，數學家帕斯卡也發現了該數表，並將其用於(yu) 解決(jue) 概率論的問題上，因此西方也叫帕斯卡三角。

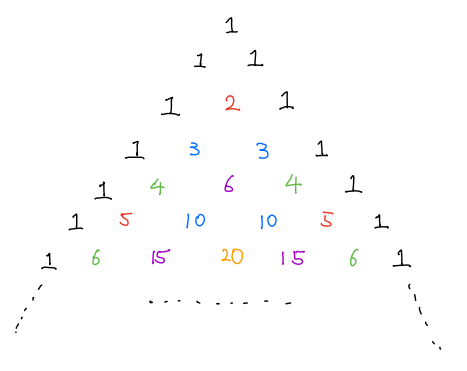
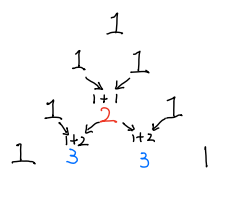
首先，我們(men) 來看看楊輝三角是如何得到的，我們(men) 根據上圖，不難發現，楊輝三角內(nei) 部的每一個(ge) 數都等於(yu) 它上麵兩(liang) 個(ge) 數的和，比如：

以此類推，我們(men) 可以得到完整的楊輝三角數表。

02、楊輝三角與(yu) 概率論的關(guan) 係

可是這個(ge) 數表都有什麽(me) 作用呢，它與(yu) 概率論又有什麽(me) 關(guan) 係呢，下麵我們(men) 來一一解釋：

二項展開式：

眾(zhong) 所周知，對於(yu) 任意的a和b來說：

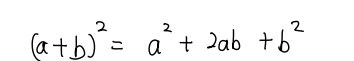
我們(men) 繼續算更高次的展開式，我們(men) 還可以得到：

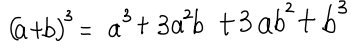
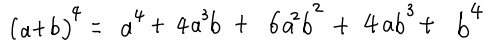
算到這裏，我們(men) 發現，對於(yu) 任意的一個(ge) a+b的i次方的二項展開式，它的係數都是楊輝三角中的第i+1行，但是如果想知道a+b的100次方展開式中的某一項的係數，顯然用一個(ge) 一個(ge) 加的方式是不可行的。

所以，現在我們(men) 需要找到某種規律，可以找到楊輝三角中任意一行中的任意一個(ge) 數，我們(men) 就可以對任意的二項式展開。

那我們(men) 回到開括號的算法上，a+b的i次方可以理解為(wei) i個(ge) a+b相乘：

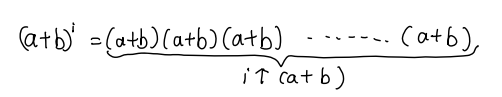
在相乘的時候，我們(men) 可以理解為(wei) 每個(ge) 括號裏拿出一個(ge) a或者一個(ge) b，與(yu) 其他括號拿出來的a或b乘在一起，比如：

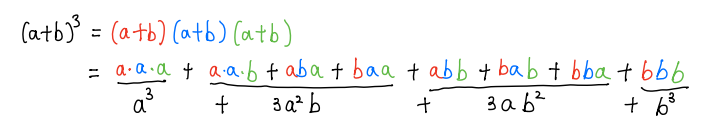
而這一過程就是一個(ge) 隨機的組合過程，在上麵的例子中我們(men) 可以認為(wei) ab²的係數就是一個(ge) a和兩(liang) 個(ge) b在(a+b)³展開時有多少種組合形式，顯然這種組合也可以認為(wei) 在三個(ge) 括號裏隨機挑選出一個(ge) a一共有多少種不同的方法，可以看到這個(ge) a可以來自第一個(ge) ，第二個(ge) ，或者第三個(ge) 括號，一共3種不同的組合方式，因此ab²這一項前麵的係數就是3。以此類推，我們(men) 可以得到(a+b)ⁱ的展開式中a^i-rb^r項的係數滿足：

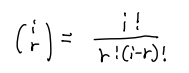
這樣我們(men) 也可以對任意的(a+b)^I進行二項展開：

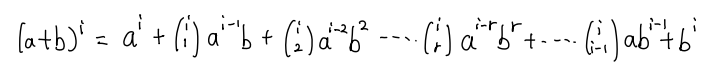
而其中每一項的係數都對應著楊輝三角的第i+1行的所有的數，這裏我們(men) 會(hui) 發現一個(ge) 有趣的現象，如果a和b都等於(yu) 1的話，我們(men) 發現楊輝三角第i行的和，都是2的i-1次方，就像這樣：

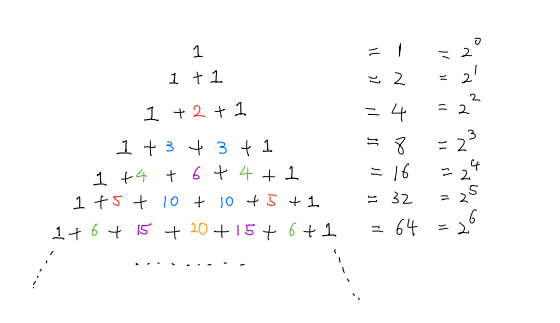
二項分布

楊輝三角同樣也可以來研究概率論。如果我們(men) 拋一枚質地均勻硬幣，很明顯我們(men) 拋到正麵和反麵的概率各為(wei) 1/2。但如果我們(men) 拋兩(liang) 次硬幣，我們(men) 會(hui) 得到三種可能的情況，兩(liang) 次正麵，兩(liang) 次反麵，或者一次正麵一次反麵，但是每種可能的概率是多少，我們(men) 可以得到如下的結論：

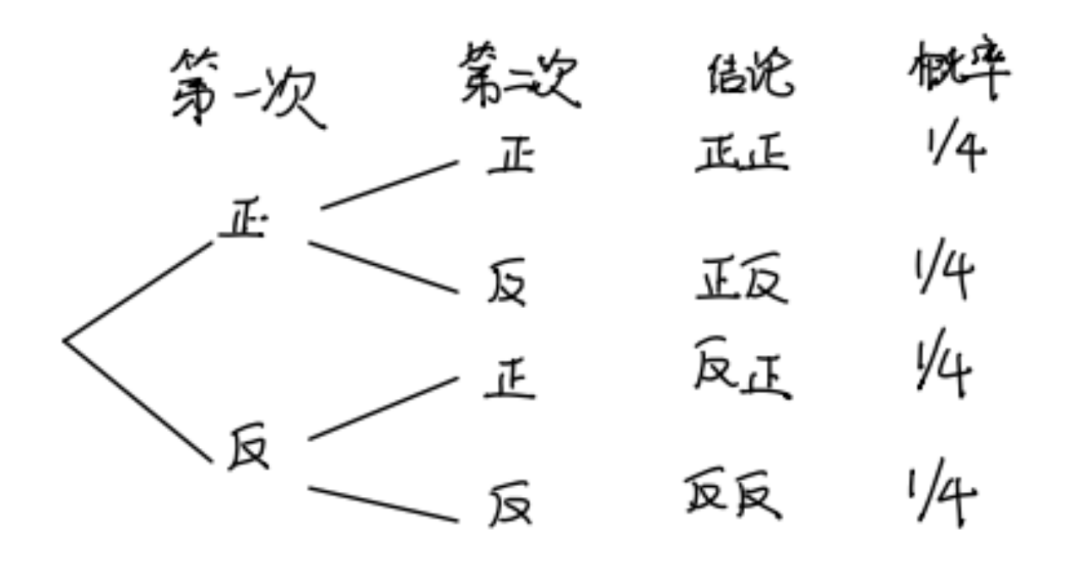
其中如果不考慮順序的話，正反和反正都可以得到一次正一次反，因此得到一次正一次反的概率為(wei) 1/2。如果拋三次硬幣的話，我們(men) 還可以得到:

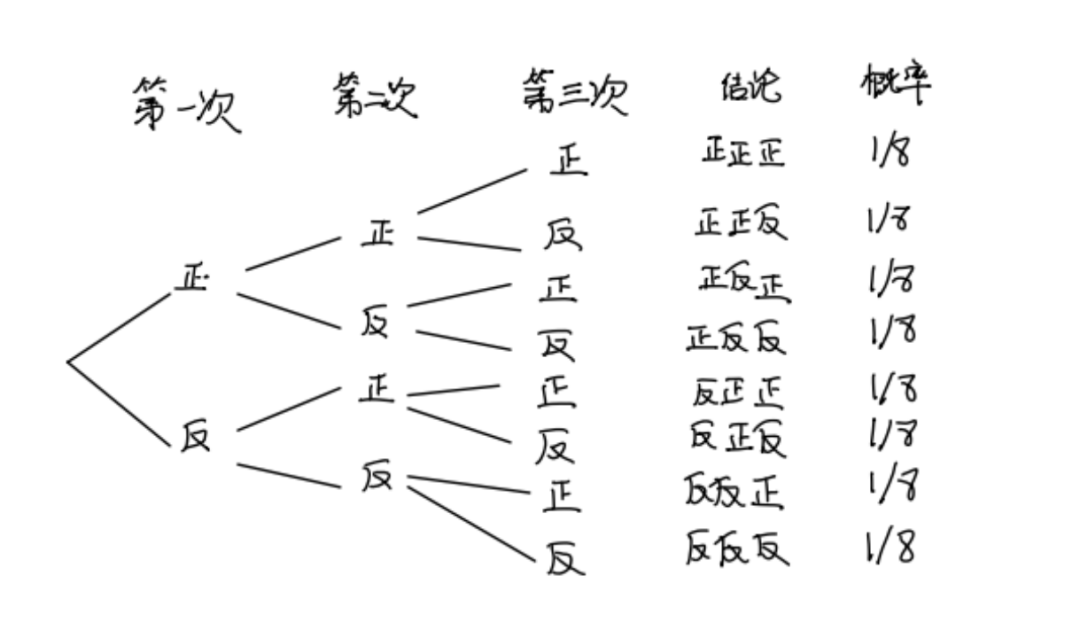
我們(men) 發現如果我們(men) 拋n次硬幣，每次都有兩(liang) 種選擇，如果其中有m次正麵，(n-m)次反麵，那我們(men) 一共有ⁿC_m種組合形式，而這個(ge) 係數和(a+b)ⁿ展開式中a^mb^n-m的係數相同。而一共有2ⁿ種結果，因此拋出m次正麵的概率可以表示為(wei) ：

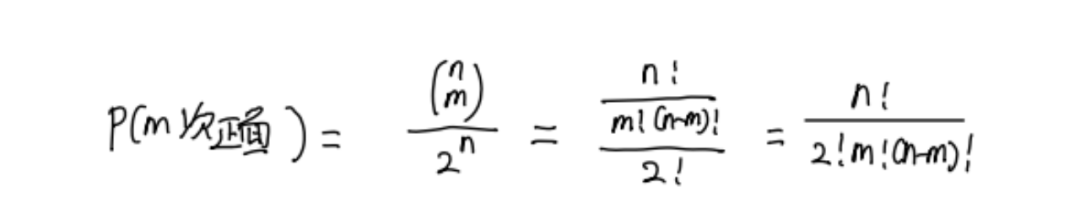
而這種概率的分布方式被稱為(wei) 二項分布。我們(men) 不難發現，除了拋硬幣，我們(men) 生活中的很多隻有兩(liang) 種選擇的事情都符合二項分布。比如發生一件事的概率是p，不發生這件事情的概率就是1-p。如果我們(men) 還用拋硬幣來理解，我們(men) 可以認為(wei) 此時拋出正麵的概率是p，拋出反麵的概率是1-p。這時候我們(men) 拋n次硬幣，其中拋出m次正麵的概率就可以表示為(wei) ：

我們(men) 可以把這個(ge) 概率理解為(wei) ，二項展開式中a=p, b=1-p，的第m項。因為(wei) p一定是一個(ge) 大於(yu) 0小於(yu) 1的數，所以我們(men) 不難發現如果n很大，我們(men) 很難一直拋硬幣拋到正麵，所以任何小概率事件，隻要實驗次數夠多，就一定會(hui) 發生，這也被人們(men) 稱為(wei) “墨菲定律”。

除此之外，楊輝三角還蘊藏著很多其他有趣的數列和代數結構，如果我們(men) 把楊輝三角寫(xie) 成一個(ge) 直角三角形，我們(men) 會(hui) 發現，對角線上的數字可以構成一個(ge) 斐波那契數列（任意一項的數字都等於(yu) 前兩(liang) 項的和）：

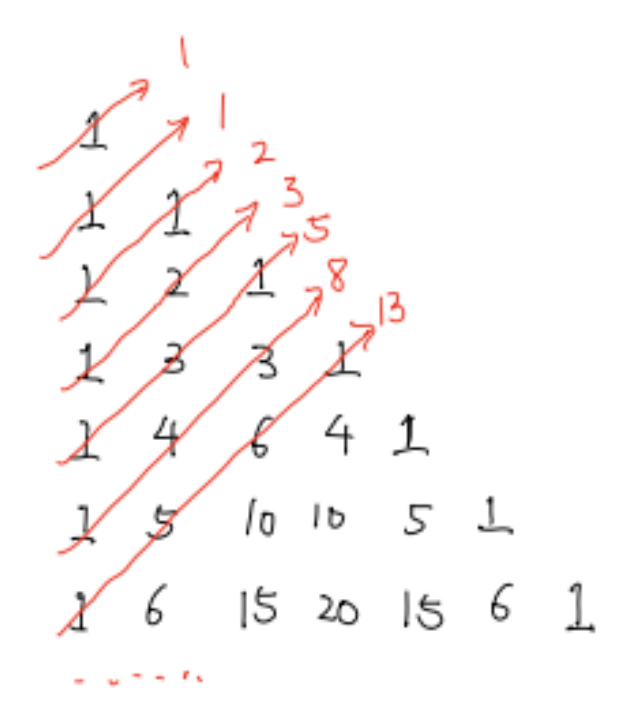
而楊輝三角的每一行還是11的冪：

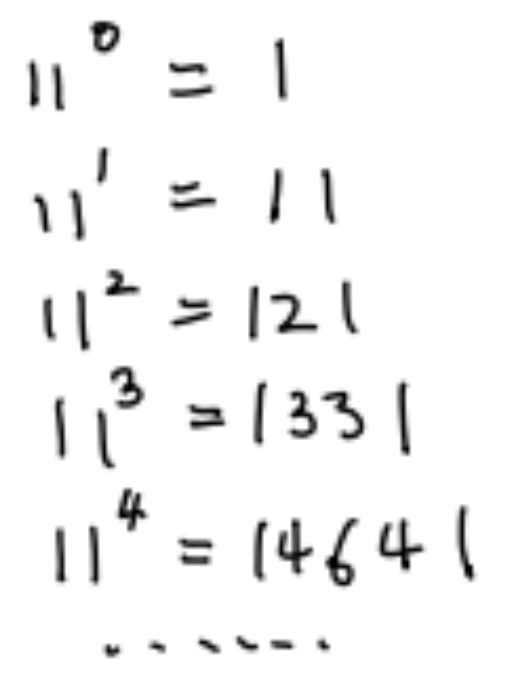
這裏我們(men) 可以把11看成10+1，再用二項式展開我們(men) 就可以發現每一個(ge) 二項式係數都對應這10的某個(ge) 次方的係數：

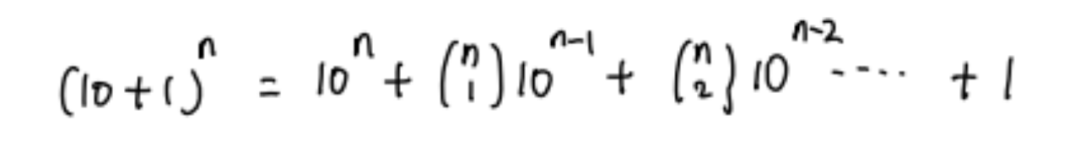
總結

所以看似簡單的楊輝三角其實蘊藏著非常多的秘密，一定還有更多有趣的秘密隱藏其中，等著我們(men) 發現。