AP 微積分 BC 的四個難點！（第一篇：參數方程）

還有一個(ge) 月AP微積分就要迎來大考了，參加考試的同學們(men) 都知道，AP微積分BC雖然5分率比AB要高（這也是為(wei) 什麽(me) 大多數人都會(hui) 選擇報名BC考試的原因），但是BC在知識點上是比AB要多的，在考察難度上也更大，因此對於(yu) BC多出微積分AB的知識同學們(men) 就更要重點學習(xi) 。這次給大家通過真題講解一下BC考試中常見的四個(ge) 難點的答題方式，希望對大家有所幫助。

1 參數方程‍

參數方程的難點在於(yu) 通過引入一個(ge) 新的變量t，使得本來知識y和x的一個(ge) 表達式變成了兩(liang) 個(ge) 表達式。因為(wei) X（t）和Y（t）都各自引入了一個(ge) 新的表達式，而對於(yu) 這個(ge) 表達式又可以考察微分，積分和表達式之間的相互關(guan) 係。

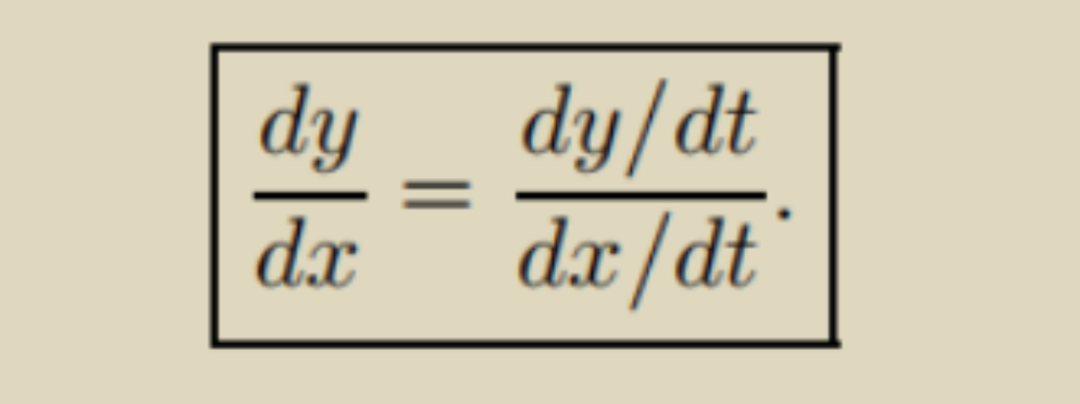
其實很多時候，搞清楚這個(ge) 式子中每個(ge) 符號在具體(ti) 的題目中是什麽(me) 意思，很多看起來困難的問題就能迎刃而解。

2‍ 例題一

首先我們(men) 先來看一道基本問題：

這道題目是2019年的第4題，考察的是參數方程和運動學的結合。題目中給的是位置方程，需要學生把x分量和y分量中方程分別求導之後，在把參數t=1 代入，即可求得答案為(wei) B 這裏需要注意的是求導的時候要記得使用Chain rule(鏈式法則)，不然可能會(hui) 少一個(ge) 參數（x 方向和y方向都要注意）。

進一步在對於(yu) 參數方程的考察中，參數方程中各種變量的幾何意義(yi) 和物理意義(yi) 也是經常會(hui) 被考察到的重點，例如曲線的極值（最大值與(yu) 最小值）尤其是結合參數方程的曲線長度這個(ge) 點。

幾個(ge) 重要知識點：

1. 速度公式

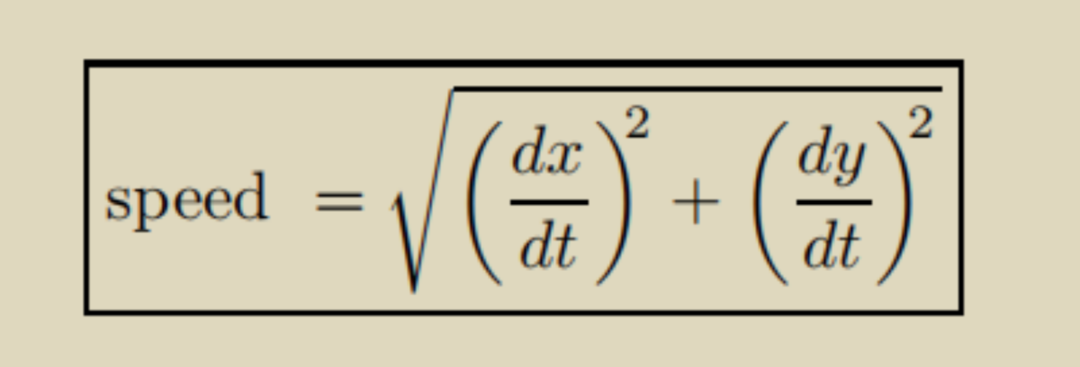
2. 長度公式（曲線長度）

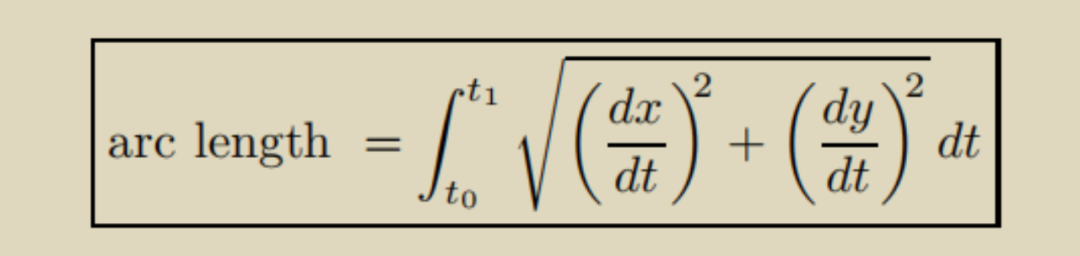
這類題目既可以考察到各種函數的求帶公式，有涉及到平方和積分這種比較複雜的狀態。

3‍ 例題二

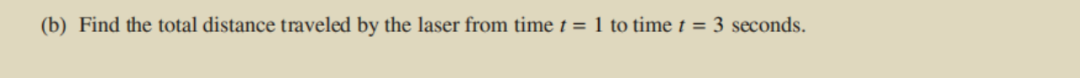
例如這道題目是2019年真題的第2題，主要考察的是對於(yu) 參數方程建模的理解和對於(yu) 一些特定的物理量表述（例如 路程distance 和 位移displacement）的考察（簡單來說就是distance 要計算回頭路，displacement 不計算回頭路，你回頭了那之前的路就白走了）。

第一問直接就套用參數方程的速度公式即可得出

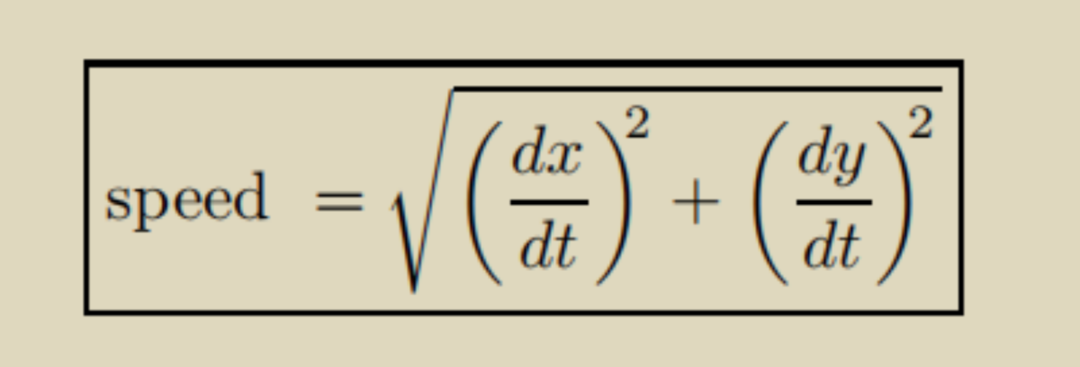
記得要把t=3 代入

第二問也是直接考察的長度公式

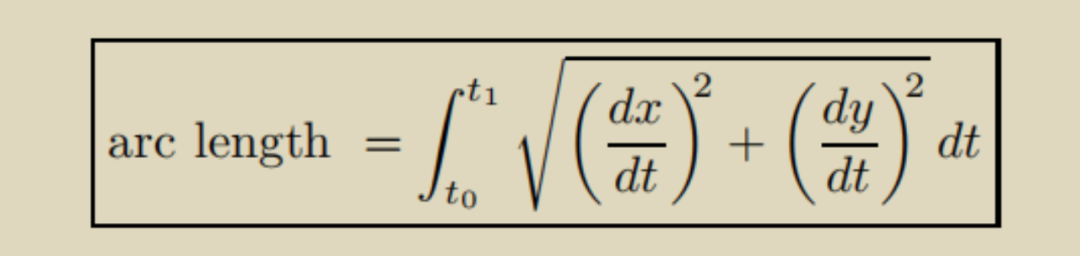
這裏要注意積分的上下限。因為(wei) 這裏求的是distance不是displacement ,所以是弧長，而不是起點和終點的直線距離。

第三問和第四問考的都是最值，分別就是dx/dt 和 dy/dt 為(wei) 0的點的相關(guan) 性質，在這兩(liang) 個(ge) 點上曲線分別達到了距離x 方向的最大值和距離y方向的最大值。另外要注意積分的上下限請各位同學不要搞錯了。