AMC 10 備考代數板塊公式、定理、方法匯總

代數是 AMC 10 中的主幹和核心部分。同時代數也是中學數學的核心思想轉變，用抽象符號關(guan) 係代替具體(ti) 的數值計算。

其實我們(men) 已經在課內(nei) 學習(xi) 了很多這一部分的公式定理。今天我們(men) 來總結一下其中那些可以幫助我們(men) 解決(jue) AMC 10 代數問題的定理。

韋達定理 （Vieta's Formula）

算數平均-幾何平均不等式 （Arithmetic Mean-Geometric Mean Inequality）

二項式定理 （Binomial Theorem）

合分比定理 （Partition Ratio Theorem）

餘(yu) 數定理（Polynomial Remainder Theorem）

1韋達定理 （Vieta'sFormula）

學習(xi) 過一元二次方程的同學一定都聽說過這個(ge) 定理，可以得出兩(liang) 個(ge) 根之間和的關(guan) 係，積的關(guan) 係。

事實上不僅(jin) 僅(jin) 是二次方程，韋達定理還可以拓展到更高階次，描述一元 n 次多項式根的關(guan) 係。著實是一個(ge) 應用麵非常廣的定理。

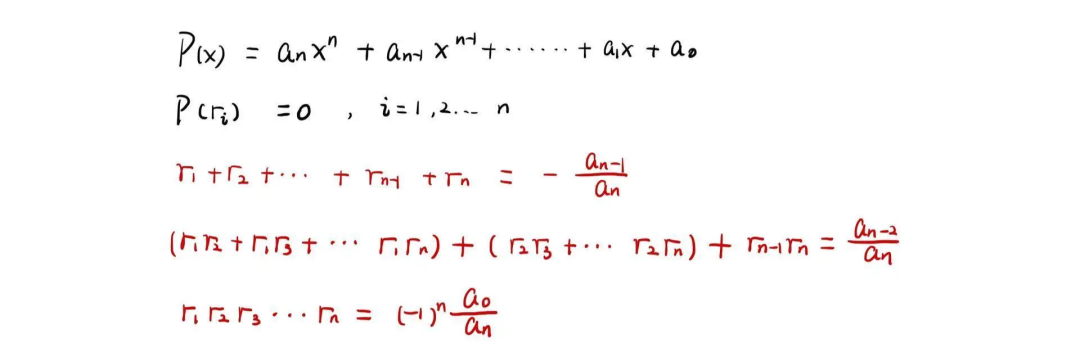
遇到多項式的問題，同時已知根的關(guan) 係，不妨想想可不可以用韋達定理來求解。對於(yu) 高次方程，韋達定理真的是一個(ge) 解題的捷徑。

AMC 10A 2019 Q24 （答案見最後）

 2、算數平均-幾何平均不等式（Arithmetic Mean-Geometric Mean Inequality）

這個(ge) 不等式是對課內(nei) 所學平方和不等式的一個(ge) 拓展。同時這個(ge) 不等式還可以和算數平均，幾何平均這兩(liang) 個(ge) 統計學概念一起進行記憶。

AMC 10 的題目一題多解是很普遍的，有時候從(cong) 一個(ge) 不同的方向去理解題目，也許是事半功倍。比如下麵這道理，利用不等式的概念可以實現快速解題。你發現了麽(me) ？

AMC 10B 2016 Q16 （答案見最後）

3二項式定理 （Binomial Theorem）

由二次多項式拓展出的結論真的很豐(feng) 富。掌握了二項式定理，從(cong) 此再也不怕二項式展開了。

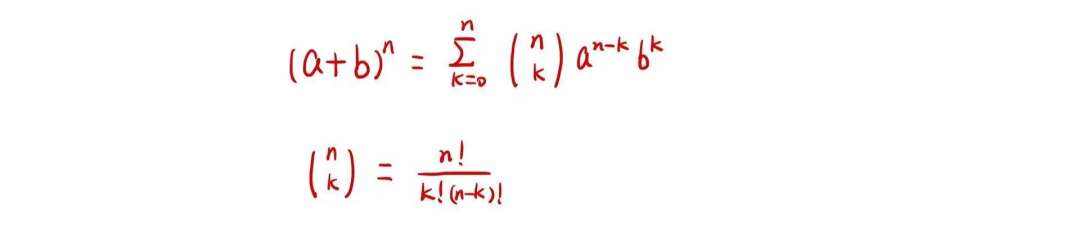
不僅(jin) 如此，結合楊輝三角，這個(ge) 定理的結論記得更牢。這裏我再附上一個(ge) 楊輝三角（Pascal triangle）。

剛剛接觸二項式定理的同學們(men) ，有沒有發現這個(ge) 三角形中隱藏的奧秘呢？

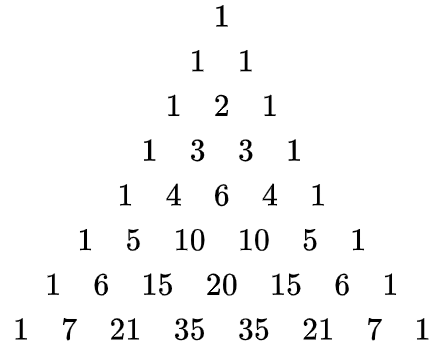
來看看下麵這道 11 年 AMC 10 的倒數第三題是如何用二項式定理一步道破天機的吧。

AMC 10B 2011 Q23 （答案見最後）

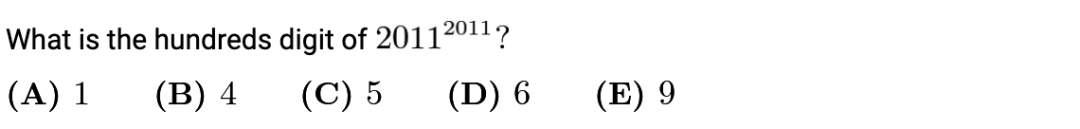
4合分比定理 （Partition Ratio Theorem）

這個(ge) 定理的形式有很多種，這裏我給出了主要的幾個(ge) 等式以及一個(ge) 不等式的推論。

無論是在代數，還是幾何問題中，根據已知比例求比例的問題，都可以嚐試用合分比定理作為(wei) 解題的核心思路。

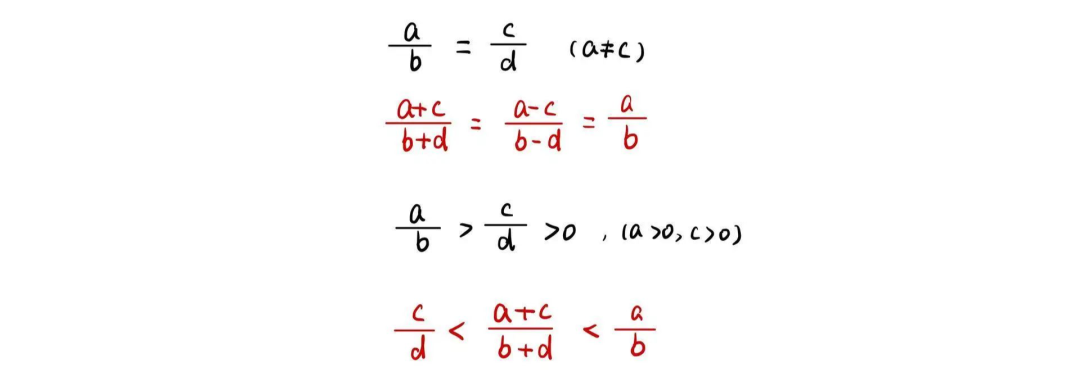
AMC 10A 2018 Q14 （答案見最後）

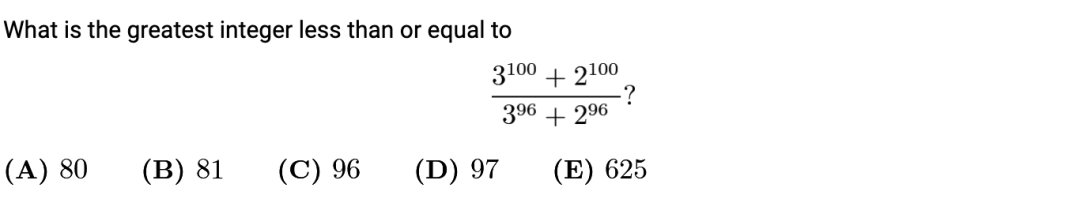
5餘(yu) 數定理（Polynomial Remainder Theorem）

我們(men) 總說魔鬼藏在細節中，一個(ge) 中學階段看似普通的定理，其結論和延伸出的因式定理在處理多項式的問題時，有時有著意想不到的功效。

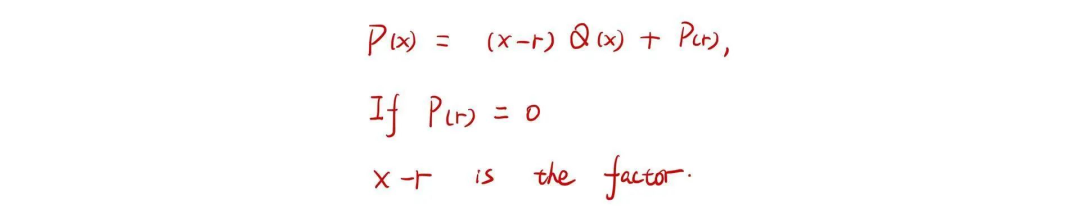
AMC 10A 2017 Q24 （答案見最後）

 詳細過程及答案