在 Alevel數學 P4模塊中,反證法的考核分值近年來呈上升趨勢,並且題型考點方麵也體(ti) 現出了更強的綜合性。牛頓曾經說過:“反證法是數學家最精當的武器之一”。那麽(me) 何為(wei) 反證法?
書(shu) 中如此定義(yi) :”To prove a statement by contradiction you start by assuming it is not true.“反證法指的是對題設肯定,而對結論否定,若在此過程中推出明顯矛盾 (主要包括與(yu) 題設的矛盾,與(yu) 已知定義(yi) ,公理和性質的矛盾),進而得出原命題成立,這便是反證法的本質思想。本篇將由理綜教研部老師為(wei) 大家以真題梳理的方式解讀反證法的攻分策略。
反證邏輯
真題梳理
相較於(yu) 教材中亢長的定義(yi) ,理綜教研部的 P4講堂上會(hui) 結合一些生活中通俗易懂的實例,如證明某餐館很受歡迎。第一步先否定結論做出反設:該餐館不受歡迎。第二步,推理出若該餐館不受歡迎,那麽(me) 周末晚間一定是空蕩蕩的,但這與(yu) 小明每次去該餐館都輪不到位置的事實相矛盾。第三步,由此可推出該餐館確實是受歡迎的。簡而言之,可把反證過程簡要概括為(wei) 三步,即“否定結論 - 推導矛盾 - 結論成立”。
答題格式:
 來源:理綜教研部 P4模塊專(zhuan) 項講義(yi) 截圖
來源:理綜教研部 P4模塊專(zhuan) 項講義(yi) 截圖
根據理綜教研部整合曆年真題,發現自2021年 10月份起,P4模塊中反證法分值設置從(cong) 原本的3分增加到了 6分,而自2022年起,考察也不再局限於(yu) 書(shu) 本例題,考點更具綜合性,靈活涵蓋純數中其他知識點。綜合以上兩(liang) 大趨勢,P4講堂在講解反證法解題步驟的同時,更加注重真題的出題邏輯,結合“每課一證”的教學計劃,引導滲透反證法的思想,從(cong) 而形成認知與(yu) 應用的螺旋式上升。根據曆年真題整合,Prove by Contradiction的題型常見的邏輯證明核心矛盾主要體(ti) 現在與(yu) 已知條件矛盾;與(yu) 已知公理、定義(yi) 、定理或公式矛盾;與(yu) 反設矛盾。
『與(yu) 反設,已知條件矛盾』
用反證法證明不存在最大奇數 (2021年 5月真題,書(shu) 本 Example 1原題)
 來源:理綜教研部 P4模塊教材截圖
來源:理綜教研部 P4模塊教材截圖
用反證法證明數的奇偶性以及數的倍數 (2020、2022年 5月真題,書(shu) 本 Example 2變形題)
例題 1
 來源:理綜教研部 P4模塊教材截圖
來源:理綜教研部 P4模塊教材截圖
例題 2 來源:2020年 5月 P4模塊真題
來源:2020年 5月 P4模塊真題
此類證明 be divisible by 4等價(jia) 於(yu) multiple of 4,則可用代數 4k表示,然後根據三步法則寫(xie) 出正確解題步驟,如下所示:
 來源:理綜教研部 P4模塊專(zhuan) 項解析截圖
來源:理綜教研部 P4模塊專(zhuan) 項解析截圖
用反證法證明質數的個(ge) 數是無限的 (理綜教研部內(nei) 部模擬卷,書(shu) 本 Example 4原題)
 來源:理綜教研部 P4模塊教材截圖
來源:理綜教研部 P4模塊教材截圖
該題的重點是理清質數 Prime Number的概念,質數隻能被 1和其自身整除,如上圖解答所示,N要麽(me) 是質數 (因為(wei) 不能被其他數整除)或N中有一個(ge) 質數因子不在已列出的質數裏,由此和反設矛盾,原命題得證。
『與(yu) 已知公理、定義(yi) 、定理、公式矛盾』
用反證法證明有理數 (2021年 10月真題,書(shu) 本 Example 3變形題)
 來源:2021年 10月 P4模塊真題
來源:2021年 10月 P4模塊真題
 來源:理綜教研部 P4模塊教材截圖
來源:理綜教研部 P4模塊教材截圖
該題重點為(wei) 理清有理數概念,有理數通常可表示為(wei) 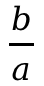 ,where a and b are integers with no common factor。接下來證明中隻需證明 a 和b存在 common factor即可得證。同理在 2023年 5月卷中,考察了證明
,where a and b are integers with no common factor。接下來證明中隻需證明 a 和b存在 common factor即可得證。同理在 2023年 5月卷中,考察了證明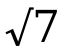 無理數,方法如上,同理可證。
無理數,方法如上,同理可證。
用反證法證明數列的等差等比性 (2022年 1月真題,結合 P2知識點)
 來源:2022年 1月 P4模塊真題
來源:2022年 1月 P4模塊真題
該題結合 P2等比數列綜合考察,重點是明確等比數列的定義(yi) :後一項與(yu) 前一項的比值相等。然後根據三步法則寫(xie) 出正確解題步驟,如下所示:
 來源:理綜教研部 P4模塊專(zhuan) 項解析截圖
來源:理綜教研部 P4模塊專(zhuan) 項解析截圖
用反證法證明不等式恒成立問題 (2022年 1月、2022年 10月真題,結合 P1知識點)
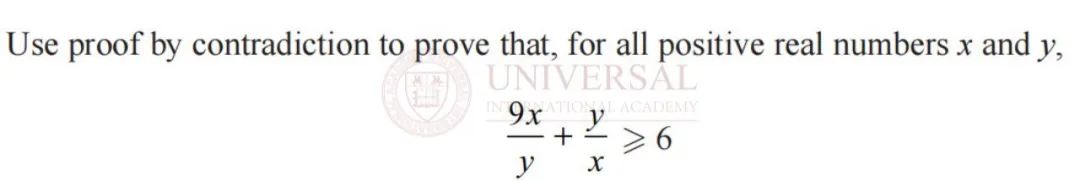 來源:2022年 1月 P4模塊真題
來源:2022年 1月 P4模塊真題
該題型是近年來常考題型,通常采用 P1 Completing the Square配平方推出與(yu) 平方數大於(yu) 等於(yu) 零相矛盾,從(cong) 而得證,然後根據三步法則寫(xie) 出正確解題步驟,如下所示:
 來源:理綜教研部 P4模塊專(zhuan) 項解析截圖
來源:理綜教研部 P4模塊專(zhuan) 項解析截圖
以下列出未考察題型,均收錄於(yu) 理綜教研部 P4模塊專(zhuan) 題練習(xi) 冊(ce) 中,可根據以上解題邏輯嚐試作答,具體(ti) 詳解可聯係理綜教研部 P4模塊老師。一月考季大幕即將拉開,預祝各位考生能夠在接下來的衝(chong) 刺階段完成充分的準備,以最飽滿的狀態迎接統考。















評論已經被關(guan) 閉。