怎麽證明萬有引力？

大家想必都聽說過牛頓和蘋果樹的故事。牛頓為(wei) 了躲避瘟疫回到鄉(xiang) 下，睡在蘋果樹下，結果被蘋果砸到。牛頓就想到：“為(wei) 什麽(me) 蘋果都是往下掉，而不是往天上掉呢？”進而提出了萬(wan) 有引力定律：物體(ti) 彼此之間都互相的吸引力，這個(ge) 力和兩(liang) 個(ge) 物體(ti) 的質量都成正比，和兩(liang) 個(ge) 物體(ti) 的距離的平方成反比。也就是：

牛頓當時並沒有得到比例係數G的值。而且，為(wei) 啥一定就是所有的東(dong) 西之間都有引力呢？有沒有可能是隻在地球和別的物體(ti) 之間存在吸引力呢？

01卡文迪許扭秤實驗

為(wei) 了證明萬(wan) 有引力的存在，並且測量萬(wan) 有引力常數的大小，卡文迪許設計了扭秤實驗。

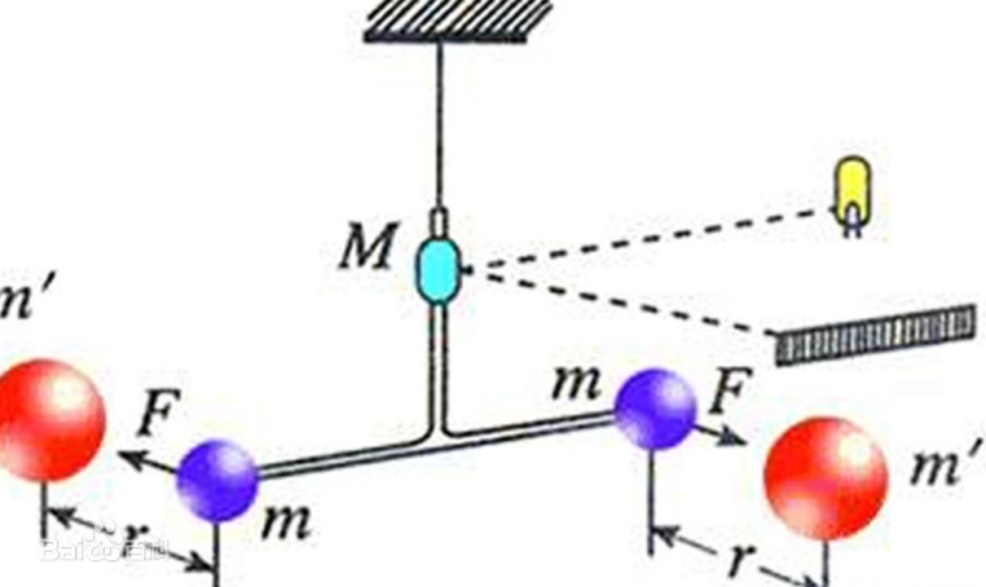
卡文迪許在一個(ge) 密閉的房間內(nei) ，將小金屬球係在長為(wei) 6英尺木棒的兩(liang) 邊，並用金屬線懸吊起來。再將兩(liang) 個(ge) 350磅的銅球放在相當近的地方，以產(chan) 生足夠的引力讓啞鈴轉動，並扭轉金屬線。

在金屬線上，卡文迪許放置了一麵老師子。啞鈴轉動之後，帶著鏡子轉動，從(cong) 而讓遠處射向鏡子的光線，反射到牆上的光點位置也跟著發生變化。

就算離得很近，銅球和小金屬球產(chan) 生的作用力依然非常小，因此卡文迪許設計了三重放大作用，來放大球和球之間的萬(wan) 有引力的影響。第一重是通過放置兩(liang) 個(ge) 球，兩(liang) 邊各自產(chan) 生作用，把力的左右轉變為(wei) 力矩作用，從(cong) 而將力臂作為(wei) 第一重放大杠杆。

第二重是將金屬線的轉動，通過反射鏡放大為(wei) 二倍，將反射轉角作為(wei) 第二重放大杠杆。第三重就是通過光線傳(chuan) 播的時候，角度轉變產(chan) 生的距離等於(yu) 弧度變化值乘以半徑，將傳(chuan) 播半徑作為(wei) 第三重杠杆。

02萬(wan) 有引力得到證明

卡文迪許的實驗設計的十分精巧，但是感興(xing) 趣的同學可以自己試一試，越是精巧的實驗就越容易遇到各種問題產(chan) 生誤差，導致失敗。卡文迪許的實驗也重複了很多次，才得到了滿意的結果。比如卡文迪許為(wei) 什麽(me) 一定要放在密閉的房間裏，就是因為(wei) 一點小小的氣流幹擾，就可能導致實驗完全失敗。

扭秤實驗最後成功觀察到了金屬絲(si) 的轉動，從(cong) 而論證了萬(wan) 有引力的存在，並且測量除了精度相對較高的萬(wan) 有引力常數。聰明的讀者們(men) 可以開動腦筋，還能不能想到啥別的證明萬(wan) 有引力存在的方法嗎？感興(xing) 趣的讀者可以私信老師進行交流。