信奧與數學有什麽關係？數學一般般能學習C++編程麽？

數學不好能學信奧嗎？

為(wei) 什麽(me) 信奧、C++編程學習(xi) 的入門測試是數學題？

學信奧前數學到底要到什麽(me) 程度？

……

許多家長都會(hui) 聽到信奧學的好，數學也要好，但也會(hui) 困惑：信奧與(yu) 數學有什麽(me) 關(guan) 係？

今天給大家稍微數理下，同時在文後也有信奧CSP-J/S認證考試相關(guan) 的數學知識匯總。

算法來源於(yu) 數學思維

在信奧領域，算法與(yu) 數據結構的學問遠遠超越了單純的編程技術。它們(men) 實際上觸及了眾(zhong) 多學科的邊界，尤其值得注意的是，算法與(yu) 數學思維的聯係是密不可分的。 探究其起源，我們(men) 會(hui) 發現算法本質上是數學思維的產(chan) 物，而編程則可以被視為(wei) 一種應用數學與(yu) 計算機科學相結合的方法，用以攻克實際問題。在信息學競賽的舞台上，數學的多個(ge) 分支——包括組合數學、數論、圖論、動態規劃以及運籌學——都扮演著不可或缺的角色。

信奧與(yu) 數學，相輔相成，相互增益

數學能力出眾(zhong) 的孩子在信奧的賽場上往往能夠如虎添翼。數學不僅(jin) 是邏輯推理能力的試金石，更是孩子們(men) 思維活躍、基礎紮實的明證。當他們(men) 投身於(yu) 編程的海洋，就像是魚兒(er) 找到了水，能夠暢快淋漓地遨遊。

反過來，信奧的學習(xi) 也如同一股清泉，滋養(yang) 著孩子們(men) 的文化課程，尤其是數學。在算法的探索之旅中，孩子們(men) 的邏輯分析能力、歸納總結技巧、數據建模的洞察力以及抽象思維的深度，都將得到同步鍛煉和提升。經過一段時間的信奧訓練，孩子們(men) 的數學能力就像被施了魔法一樣，自然而然地飛躍提升。

數學成績一般般，可以學信奧麽(me)

‍目前數學成績一般般，往往是指校內(nei) 的數學考試成績。這個(ge) 不能作為(wei) 唯一的判斷依據，孩子可以先經過數理邏輯測評再來判斷，是直接進入C++的學習(xi) 還是先通過Python編程進行過渡。並且C++的語法階段，對於(yu) 數學要求不高。C++編程和數學就像兩(liang) 條腿，我們(men) 可以先邁一條，等另一條跟上。‍‍‍‍‍‍‍

需要提前學習(xi) 數學嗎

盡管提前涉獵數學並非絕對必要，但對於(yu) 學有餘(yu) 力的學生來說，提前探索數學的奧秘無疑是一種寶貴的投資。數學與(yu) 信息學競賽在很多方麵是相輔相成的。若想在信奧的征途上走得更遠，積累豐(feng) 富的數學知識是不可或缺的。

掌握比當前階段更深層次的數學知識，將為(wei) 你的競賽之路打下堅實的基礎。麵對一道棘手的難題，如果你的數學知識庫足夠充實，你就能像站在山頂俯瞰山穀一樣，從(cong) 更高的視角審視問題，從(cong) 而讓原本複雜的問題變得條理清晰、簡單易懂。

如何補充數學儲(chu) 備

可以閱讀相關(guan) 書(shu) 籍，如《信息學奧賽之數學一本通》、《組合數學》、《線性代數》等；還可以對照CSP-J/S考試要求、NOI大綱等，針對性地補充信奧比賽中提到的數學知識。還有像程序員愛逛的CSDN裏也有很多大牛整理過很詳細的“信奧中的數學”相關(guan) 的資料。（這些資源，新手家長，都可以文末掃碼進群來交流）‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍

信奧的數學知識點分布

歸根溯源，信奧對學生的數學知識儲(chu) 備到底有什麽(me) 要求，我們(men) 來看下CCF 官方發布的《全國青少年信息學奧林匹克係列競賽大綱》（下簡稱 NOI 大綱），在入門級就對選手們(men) 明確提出了以下知識點的考察要求：

首先，紮實學習(xi) 課內(nei) 的數學，甚至提前進度，是順利學習(xi) 信奧賽的前提。以上麵提到的入門級考察的“數及其運算”為(wei) 例，考綱要求入門級選手熟知數的概念與(yu) 各類算術運算，包括四則運算與(yu) 取餘(yu) 運算。

其實這一要求並沒有偏離課內(nei) 數學的要求，課內(nei) 知識與(yu) 信奧賽入門階段的學習(xi) 可以說是相輔相成的。而另一個(ge) 模塊“數的進製”，看起來就稍顯進階了，畢竟課內(nei) 數學少有用到二進製乃至更加複雜的十六進製的機會(hui) ，但在信奧賽的學習(xi) 中，與(yu) 計算機打交道是信奧賽選手的家常便飯。不過有經曆的信奧學員知道：實際上將十進製與(yu) 二進製，甚至是其他各類進製的數字進行互轉，其實隻需要使用到上麵提到的四則運算與(yu) 取餘(yu) ，這是數學知識幫助到信奧賽的應用例子之一。

信奧CSP-J/S認證中的數學知識體(ti) 係

當然，NOI是高中生才參與(yu) ，入門級的CSP-J/S認證以初中生為(wei) 主，小學生為(wei) 輔。這兩(liang) 個(ge) 群體(ti) 在同台競爭(zheng) 時，初中生能有知識麵與(yu) 經驗更加豐(feng) 富的微弱優(you) 勢。

所以要想在CSP認證尤其是提高組（CSP-S）中獲得好成績，提前接觸初中的數學知識也必不可少。例如下麵CSP的模擬練習(xi) 題，就涉及到了一元二次方程的解法，而正常來說，這是在初三階段才會(hui) 學習(xi) 到的知識。

以下是CSP-J/S認證考試，入門組和提高組分別會(hui) 涉及到的數學知識模塊，大家可以收藏下來作為(wei) 參考：

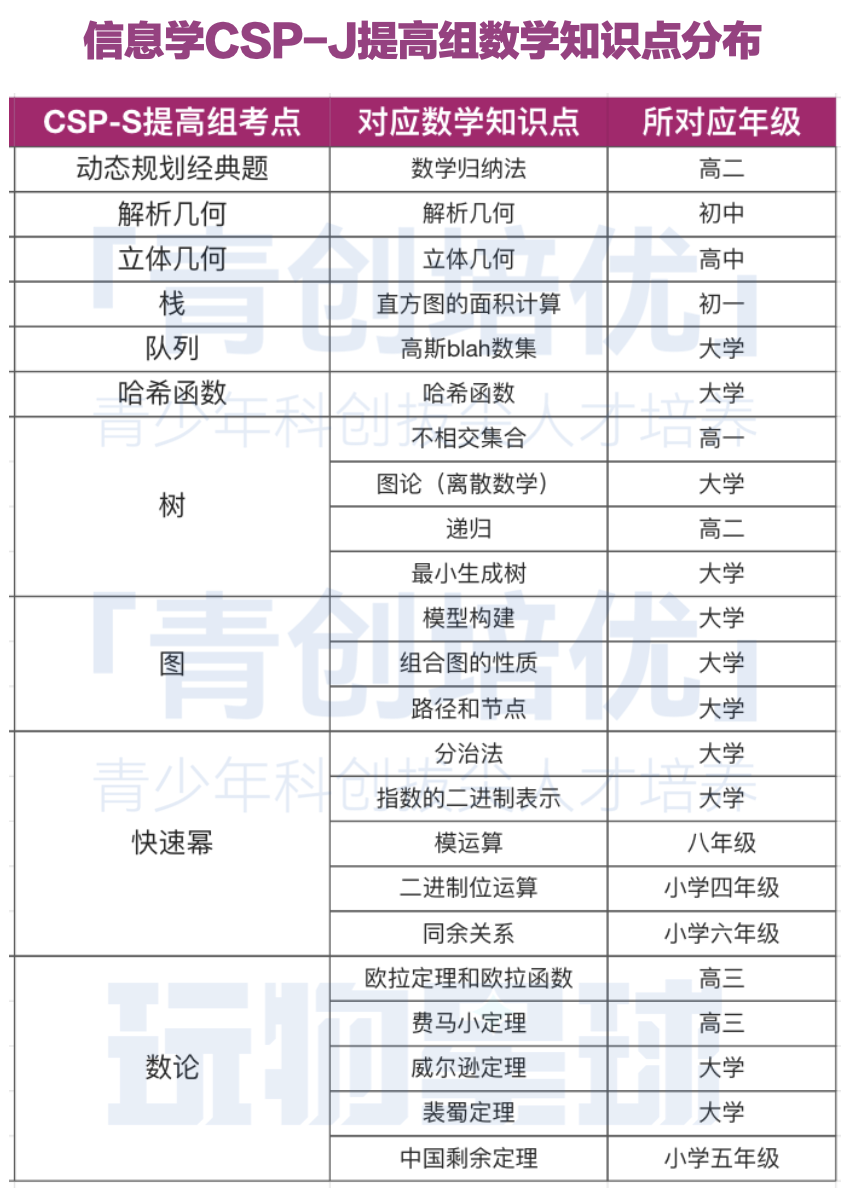
為(wei) 了便於(yu) 理解這些數學知識的層級，我再根據年級，做一下對應：

CSP-J入門組數學內(nei) 容分年級

一、小學部分的知識

1、數與(yu) 運算

‍認識自然數，掌握基本的加法、減法、乘法、除法運算規則。

理解分數和小數的基本概念，進行簡單的分數和小數的加減乘除運算。

學習(xi) 整數的加減法，特別是負數的概念和運算。

掌握數的比較和大小排序，理解絕對值的概念。

2、幾何圖形

理解點、線、麵的基本構成，識別和繪製基本的二維幾何圖形。

學習(xi) 不同圖形的性質，例如三角形的分類（等邊、等腰、直角三角形）和四邊形（正方形、長方形、菱形、梯形）的性質。

掌握對稱性的概念，包括軸對稱和中心對稱，以及圖形的平移、旋轉和翻轉。

3、簡單邏輯

理解基本的邏輯連接詞，如“和”、“或”、“不”。

通過簡單的邏輯推理題來鍛煉邏輯思維能力。

學習(xi) 基本的條件判斷，如“如果...那麽(me) ...”的推理模式。

二、初中部分的知識

1、代數基礎

引入變量的概念，理解代數表達式的構成和簡化。

學習(xi) 一元一次方程的建立和解法，解決(jue) 實際問題。

掌握不等式的基本性質和解不等式組的方法。

理解線性函數的概念，包括函數的圖像和斜率。

2、幾何進階

深入學習(xi) 角的概念，包括角的度量、角的分類和角的性質。

掌握多邊形的麵積和周長計算公式，理解如何通過分割和組合來計算複雜圖形的麵積。

學習(xi) 圓的基本性質，包括圓周角定理、垂徑定理等。

理解相似三角形的概念，掌握相似三角形的判定和性質。

3、組合數學入門

學習(xi) 排列組合的基本概念，理解排列和組合的區別和聯係。

通過實際問題來學習(xi) 簡單的計數問題，如加法原理和乘法原理。

理解二項式定理的基本形式和應用。

4、概率與(yu) 統計

學習(xi) 概率的基本概念，包括隨機事件和概率的計算。

掌握簡單事件的概率計算方法，如古典概型和幾何概型。

理解基本的統計概念，如平均數、中位數、眾(zhong) 數，並能夠進行簡單的數據分析。

三、高中知識（入門組中較少涉及，但可能包含）

1、函數概念

‍深入理解函數的定義(yi) 和性質，包括函數的域、值域和圖像。

學習(xi) 常見函數的圖像和性質，如二次函數的開口方向、頂點坐標和對稱軸。

2、數列

學習(xi) 等差數列和等比數列的概念、性質和公式。

掌握數列求和的方法，如等差數列和等比數列的求和公式。

3、邏輯與(yu) 證明

學習(xi) 證明的基本方法，如直接證明、反證法等。

理解數學歸納法的原理，並能夠應用於(yu) 簡單的數學問題。

CSP-S提高組數學內(nei) 容分年級

一、小學部分的知識

1、基礎數學概念

‍自然數的認識和四則運算

整數、小數和分數的基本概念和運算

基本的數的比較和排序

簡單的幾何圖形識別（點、線、麵、正方形、長方形、三角形等）

基本的邏輯推理（如簡單的條件語句）

二、初中部分的知識

1、代數基礎

變量和代數表達式的使用

一元一次方程的解法

不等式的解法

線性函數和它們(men) 的圖像

多項式的運算和因式分解

2、幾何進階

平麵圖形的屬性和分類

圓的性質和基本幾何體(ti) （如立方體(ti) 、圓柱、圓錐）

幾何證明的初步（相似三角形、四邊形的性質）

3、組合數學與(yu) 概率基礎

排列組合的基本概念

基本的計數原理

概率的簡單計算和統計基礎

4、離散數學初步

邏輯命題的真假判斷

基本的集合概念和運算

三、高中部分的知識

1、代數深入

二次方程和高次方程的解法

指數和對數函數

數列和級數

抽象代數入門（群、環、域的基本概念）

2、幾何與(yu) 解析幾何

坐標幾何和向量

三維空間的幾何基礎

幾何證明的深入（如正弦定理、餘(yu) 弦定理）

3、概率與(yu) 統計

概率分布、期望值、方差

統計學基礎（數據的收集、分析和解釋）

4、離散數學

圖論基礎（圖的遍曆、最短路徑、最小生成樹）

邏輯和布爾代數

組合優(you) 化問題

四、大學知識（高等數學內(nei) 容）

1、微積分

極限、連續性、導數和微分

積分學（不定積分和定積分）

級數（收斂性、泰勒級數）

2、線性代數

高階矩陣運算

線性方程組的矩陣解法

向量空間和線性變換

特征值和特征向量

3、數論

素數和因數分解的深入

中國剩餘(yu) 定理

費馬小定理和歐拉定理

4、組合數學與(yu) 圖論

高級組合數學（組合恒等式、生成函數）

圖論算法（圖的著色、匹配問題、網絡流）

5、概率論與(yu) 數理統計

隨機變量和分布

大數定律和中心極限定理

參數估計和假設檢驗

6、離散數學與(yu) 算法

算法複雜性分析（時間複雜度和空間複雜度）

動態規劃

貪心算法

分治算法

回溯算法

看完這篇，可能會(hui) 勸退一部分家長，但事實上，所有的學習(xi) 都是循序漸進和逐步深入的。信奧作為(wei) 五大學科競賽之一，和校內(nei) 學習(xi) 最大的區別就是，這是在某個(ge) 學科上的極致專(zhuan) 注和極致深入。

‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍所以看到這些數學體(ti) 係，不是意味著你必須要到這個(ge) 高度，畢竟能到“高處看風景”的還是少數，而我們(men) 隻需要關(guan) 注腳下，知道這一路上會(hui) 出現這些，我們(men) 會(hui) 攻克它們(men) 就行了。

最後放一個(ge) 今年信奧的各大賽事的時間表，作為(wei) “入場券”的CSP-J/S認證考試的第一輪是在9月21日。‍‍‍‍‍‍‍‍‍‍‍

暑假是重要的信奧C++入門和老學員衝(chong) 刺CSP的關(guan) 鍵時期。請大家盡早做好學習(xi) 計劃！