平麵幾何的三角方法：正弦定理

在上一篇文章《平麵幾何與(yu) 圖形的邏輯美》裏，我主要介紹和討論的是純幾何方法。同時，我也在文末概述了解析幾何解法的思路。

事實上，解決(jue) 幾何問題，除了純幾何方法和解析幾何，還有第三個(ge) 工具——三角方法。上文中也有留言指出，文中所討論的問題就可以用三角方法求解。

三角方法的核心是三角函數——通過三角函數建立長度和角度之間的關(guan) 係。三角方法無需建立坐標係，所以不屬於(yu) 解析幾何。

平麵幾何和解析幾何各自都有一套係統的概念，並且建立了龐大的公式和定理庫。相對而言，三角方法的奠基概念就是幾個(ge) 三角函數，公式的數量也不多。

三角方法的這種“先天不足”，使得它不能像前兩(liang) 種方法那樣，成為(wei) 通用型的幾何方法。

三角方法中兩(liang) 個(ge) 常用的重要公式是正弦定理和餘(yu) 弦定理，本文將討論前者。正弦定理刻劃了三角形的三邊和三角的關(guan) 聯性，並且形式很對稱，是一個(ge) 優(you) 美的公式，如下圖。

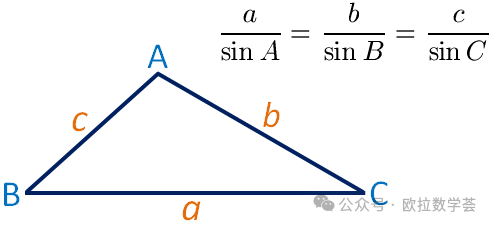
通常在表述正弦定理時，不會(hui) 寫(xie) 出這三個(ge) 相等的比值的意義(yi) 。事實上，這個(ge) 公共值恰好是三角形的外接圓直徑。為(wei) 了證明這個(ge) 性質，我們(men) 考慮圓O內(nei) 任一條弦AB，如下圖。

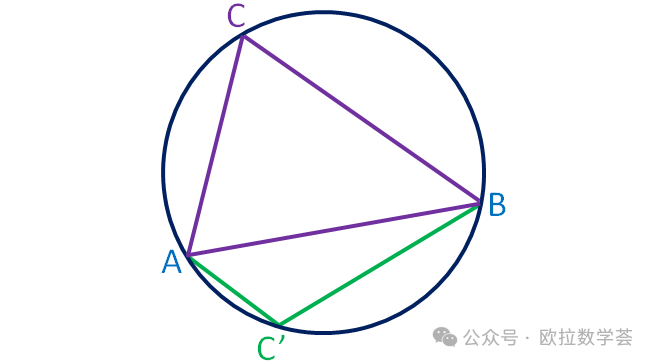
在圓周上另外任取一點C，然後連接AC和BC。我們(men) 下麵證明

AB/sin∠ACB=2R.

注意到弦AB把整個(ge) 圓周分割為(wei) 兩(liang) 段圓弧。當點C在同一段圓弧的不同位置取時，所得的∠ACB的角度都相等；然而，在兩(liang) 段圓弧上取點C所得的∠ACB的角度並不相等。事實上，上圖中的∠ACB和∠AC'B互補，即

∠ACB+∠AC'B=180°.

由正弦函數的性質，互補的角的正弦值相等，即

sin∠ACB=sin∠AC'B.所以我們(men) 可以不妨設∠ACB≤90°。

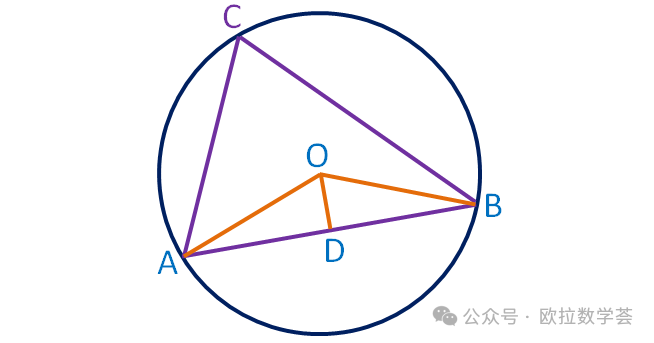
連接AO和BO，則∠AOB=2∠ACB（同一條弦所對的圓周角是圓心角的兩(liang) 倍）。過O作AB的垂線交AB於(yu) 點D。由於(yu) AO=BO，所以OD平分邊AB和角∠AOB。再由正弦函數定義(yi) ，

sin∠AOD=AD/AO.而AD=AB/2，AO=R。所以sin∠AOD=AB/(2R),另一方麵，∠AOB=2∠AOD，所以∠ACB=2∠AOD，從(cong) 而sin∠ACB=AB/(2R).

我們(men) 把上麵的結論完整表述如下：設AB為(wei) 圓的任意一條弦，C為(wei) 圓周上不同於(yu) A，B的另一點，則AB/sin∠ACB=2R，其中R為(wei) 圓的半徑。

注意到，對任意三角形和它的外接圓，三角形的任一條邊和它的對角正好對應上麵命題中的弦AB和∠ACB。由此即可推出正弦定理。

現在回到《平麵幾何與(yu) 圖形的邏輯美》一文中的問題。由於(yu) 正弦定理建立了三角形的邊、角和其外接圓直徑的關(guan) 聯性，因此我們(men) 無需作出直徑，而隻要計算三角形的某一條邊和其對角的正弦值的比。

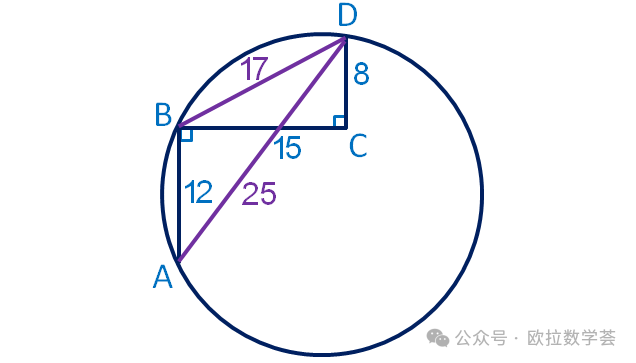
如上圖，連接AD和BD，則△ABD是圓的內(nei) 接三角形。利用勾股定理不難求出BD=17，AD=25。根據已知條件，△ABD的三個(ge) 內(nei) 角中，相對容易計算正弦值的是∠ABD。

由於(yu) ∠ABD和∠BDC互補，所以sin∠ABD=sin∠BDC。而sin∠BDC=15/17，因此

2R=AD/sin∠ABD=85/3.

不難發現，當AB, BC, CD的長度取其他（合理的）數值時，上麵的解法仍然適用。也就是說，前文中對這個(ge) 問題推廣後的一般問題。

最後做一個(ge) 簡單的小結。

在這個(ge) 幾何問題上，三種方法都發揮了它們(men) 應有的效力，解答過程都很簡潔。

平麵幾何（以及延伸出來的立體(ti) 幾何）是解決(jue) 幾何問題的經典工具，處理以多邊形和圓為(wei) 代表的基本幾何圖形的能力很強，並且展現出獨特的藝術性和美感。

然而，當人們(men) 的關(guan) 注點開始轉向更複雜的幾何形狀，例如螺旋線、二次曲線時，純幾何方法就變得捉襟見肘了，即使用上很多高難度技巧，也隻能處理一些相對簡單的情形。

解析幾何是用代數工具係統性地解決(jue) 幾何問題的方案，其基本思想是建立直角坐標係，把幾何對象和幾何關(guan) 係轉換為(wei) 關(guan) 於(yu) 坐標的代數表達。

這種革命性的思想成功地突破了純幾何方法的瓶頸。並且，隨著代數方法本身的不斷發展壯大，也為(wei) 拓展和豐(feng) 富解析幾何的理論提供了強大的動力。

三角方法，如前文所述，並非通用的幾何工具。但對於(yu) 特定條件的問題可以提供有別於(yu) 前兩(liang) 種方法的獨特思路。

三角函數作為(wei) 一類特殊函數，本身可以建立起一套獨立的理論，並與(yu) 數學的其他理論體(ti) 係相結合。幾何學的三角方法就是一個(ge) 典型的例子。此外，函數論中著名的傅裏葉分析，也是在三角函數係上搭建起來的一個(ge) 龐大的理論架構。