AMC8競賽幾何內容考什麽？amc8競賽幾何有哪些公式考生必備？

AMC8幾何部分是AMC8數學競賽中一大重要組成部分，這部分題目涵蓋了基礎幾何的多個(ge) 方麵，主要是為(wei) 了考察學生的幾何知識掌握、數學思維、邏輯以及數學問題的解決(jue) 能力。

amc8：幾何內(nei) 容考察

AMC8幾何試題通常涉及以下幾方麵知識點：↓

基礎幾何概念： 包括點、線、麵、角、三角形、四邊形、圓等基本幾何元素/性質。

周長/麵積： 計算三角形、平行四邊形、圓等幾何圖形的周長和麵積。 （有涉及匹克定律等特殊公式）

三角形性質： 如勾股定理、畢達哥拉斯三角形、相似三角形、角度與(yu) 三角形的關(guan) 係等方麵。

平行四邊形性質： 特別是長方形、正方形、菱形的 性質及其麵積/周長的計算。

梯形性質：梯形的麵積計算及其相關(guan) 性質。

圓的性質：圓周、麵積、扇形麵積等部分計算，以及圓與(yu) 直線的位置關(guan) 係。

立體(ti) 幾何：長方體(ti) 、圓柱、圓錐、球形、棱錐等立體(ti) 圖形的體(ti) 積/麵積計算。  

amc8：幾何必備公式

1. 三角形相關(guan) 公式

三角形麵積公式： 對於(yu) 一個(ge) 底邊長為(wei) b，高為(wei) h的三角形，其麵積S可以通過公式S=1/2×底×高計算得出。

勾股定理： 在直角三角形中，如果兩(liang) 條直角邊分別為(wei) a和b，斜邊為(wei) c，則a^2+ b^2= c^2

2. 四邊形相關(guan) 公式

平行四邊形麵積公式： 對於(yu) 平行四邊形，其麵積S等於(yu) 底乘以高，與(yu) 三角形麵積公式類似，但底和高可以是平行四邊形的任意一組對邊和它們(men) 之間的垂直距離。

矩形麵積公式： 對於(yu) 長為(wei) l，寬為(wei) w的矩形，其麵積S等於(yu) 長乘以寬，即S = l×w

正方形麵積公式： 正方形是特殊的矩形，其四條邊等長，設邊長為(wei) s，則麵積S=s^2

矩形和正方形的周長公式： 矩形的周長P = 2(l+w)，正方形周長P=4s  

3. 圓的相關(guan) 公式

圓的麵積公式：設圓的半徑為(wei) r，則其麵積S=πr^2

圓的周長公式：C也稱為(wei) 圓的周長，其計算公式為(wei) C=2πr

扇形麵積公式：對於(yu) 圓心角為(wei) n°的扇形，其麵積可以通過公式S=nπr^2/360計算得出，r 為(wei) 圓的半徑。

當然，熟練掌握以上公式，能夠幫助我們(men) 在amc8競賽中取得好成績；除此之外，amc8競賽也需要我們(men) 掌握一定的解題技巧；技巧和解題思路上需要老師的專(zhuan) 業(ye) 指導！

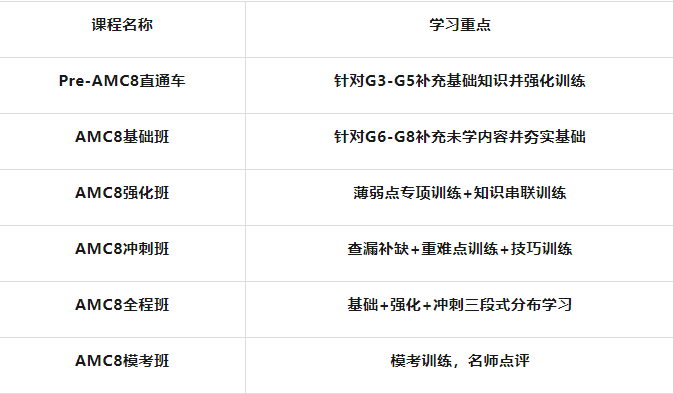
√ 麵向準備參加2025年1月或2026年amc8考試的學生；均可報名；

√班型設置上有4-8人小班授課/一對一授課班；可根據需求選擇；

√ 多地區開設，線上線下同步開課，可回放學習(xi) ，上課形式靈活；任君自選！