Bebras競賽Year 11-13級別題目詳解

準備好迎接腦力的終極考驗了嗎？Bebras競賽Year 11-13級別的題目不僅(jin) 僅(jin) 是在考你對算法和數據結構的熟悉程度，更是在向你發出智力巔峰挑戰！在這個(ge) 階段，簡單的邏輯遊戲已經不足以滿足你的“燒腦”需求，現在是時候進入更高級別的智慧競技場，麵對複雜的算法、數據結構和計算機係統問題，真正體(ti) 驗成為(wei) 一名計算機科學家的快感。PGA為(wei) 你準備了這份詳細的考點指南，讓你在輕鬆有趣中掌握競賽核心內(nei) 容，化解每一個(ge) 燒腦難題！

01、高級算法與(yu) 數據結構(Advanced Algorithms and Data Structures)

樹狀結構與(yu) 圖論 (Tree Structures and Graph Theory):

題目展示了工廠生產(chan) 流程的樹狀圖結構，要求學習(xi) 理解如何通過圖論中的樹結構來表示生產(chan) 和包裝單位之間的關(guan) 係。這在數據結構的學習(xi) 中非常重要，特別是涉及到樹和圖的表示與(yu) 遍曆。

流程優(you) 化與(yu) 路徑規劃 (Process Optimization and Path Planning):

學生需要分析每個(ge) 生產(chan) 單位如何連接以及如何將產(chan) 品送到最終的包裝單位。這類似於(yu) 路徑規劃和流程優(you) 化問題，在高級算法中應用廣泛。

資源分配與(yu) 依賴關(guan) 係 (Resource Allocation and Dependency Relationships):

題目要求理解單位之間的依賴關(guan) 係，即每個(ge) 生產(chan) 單位如何依賴於(yu) 前一個(ge) 單位，包裝單位則作為(wei) 流程的終端。這涉及到資源的分配和處理多個(ge) 依賴關(guan) 係的能力。

02、圖論與(yu) 網絡優(you) 化(Graph Theory and Network Optimization)

最短路徑問題 (Shortest Path Problem):

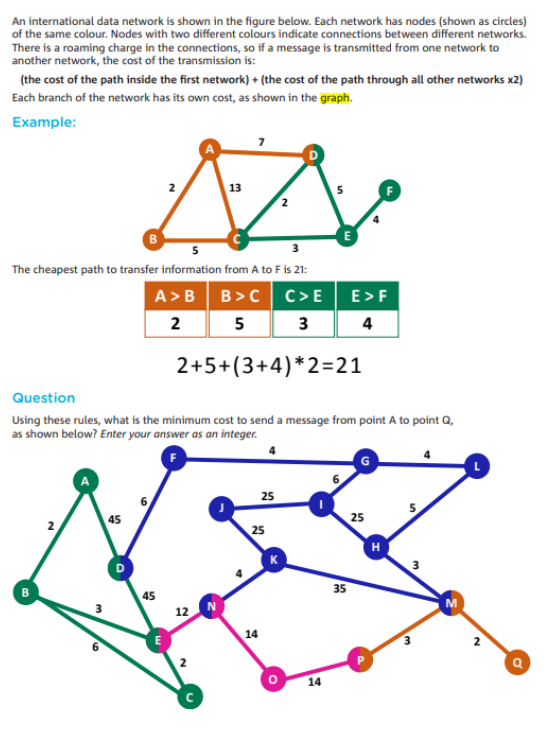
題目要求學生在一個(ge) 圖中找到從(cong) 一個(ge) 節點（A）到另一個(ge) 節點（Q）的最小傳(chuan) 輸成本。這類似於(yu) 圖論中的最短路徑問題，學生需要應用圖的遍曆算法來找到路徑，並計算其對應的總成本。

網絡傳(chuan) 輸成本計算 (Network Transmission Cost Calculation):

題目中每個(ge) 網絡的連接線都有不同的成本，且跨網絡的傳(chuan) 輸費用是雙倍的。學生需要掌握如何在圖中根據邊的權重計算路徑成本，並特別注意跨網絡的額外成本。

動態規劃與(yu) 路徑優(you) 化 (Dynamic Programming and Path Optimization):

在求解最短路徑的過程中，學生可以應用動態規劃的思想，通過比較不同路徑的成本來找到最優(you) 解。這是網絡優(you) 化中的重要技術。

03、遞歸與(yu) 動態規劃(Recursion and Dynamic Programming)

遞歸調用 (Recursive Calls):

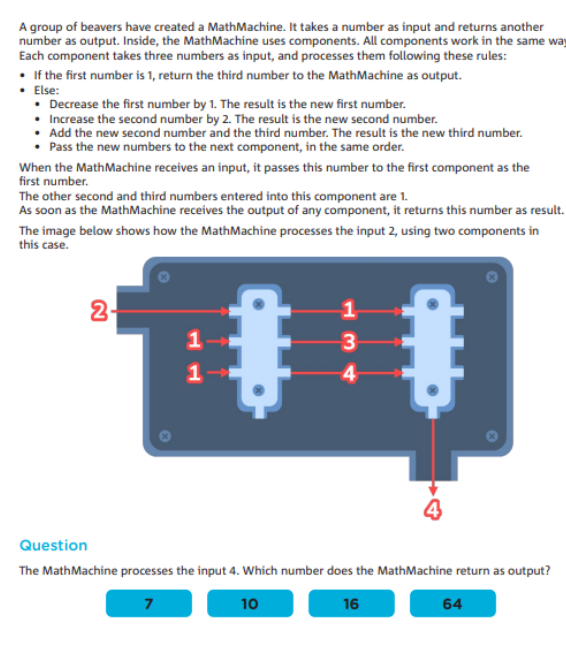
題目中的 MathMachine 是一個(ge) 遞歸結構，它根據輸入值不斷調用自身的組件，並最終輸出一個(ge) 結果。理解遞歸的工作方式對於(yu) 解答這個(ge) 題目至關(guan) 重要。

狀態轉移與(yu) 更新(State Transition and Updates):

每個(ge) 組件對輸入的數字進行狀態轉移，包括對數字的增加、減少和傳(chuan) 遞，這類似於(yu) 動態規劃中的狀態更新。在遞歸調用的過程中，組件的狀態發生變化，最終影響輸出結果。

遞歸終止條件(Recursive Termination Condition):

題目明確了遞歸終止條件：當輸入為(wei) 1 時，直接返回第三個(ge) 數字。學生需要理解這一終止條件在遞歸過程中的作用。

04、計算機係統與(yu) 並發編程(Computer Systems and Concurrent Programming)

順序執行與(yu) 結果預測 (Sequential Executionand Result Prediction):

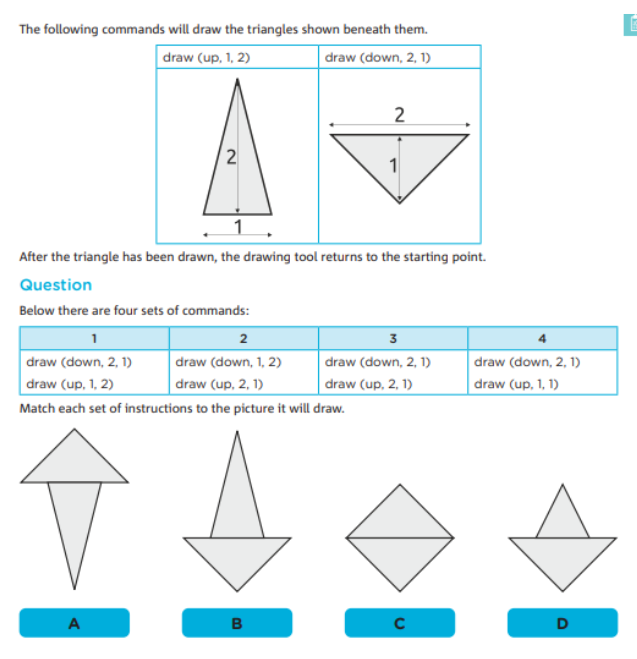
題目給出了一係列的命令，每個(ge) 命令將繪製一個(ge) 三角形。學生需要理解這些命令按順序執行後所產(chan) 生的圖形，這涉及到計算機係統中的順序執行和並發任務的順序控製。

命令的重複與(yu) 組合 (Repetition and Combination of Commands):

每組命令重複兩(liang) 次繪製三角形，然後回到起始點。學生需要根據命令的組合來預測最終的圖形，這與(yu) 編程中的循環和條件控製相似。

圖形的對稱性與(yu) 變化 (Symmetry and Transformation of Shapes):

題目涉及到對圖形的對稱性和旋轉的理解，通過繪製不同方向的三角形，學生需要識別最終的圖形形狀，這類似於(yu) 圖形編程中的坐標變換和圖形處理。

05、組合數學與(yu) 概率(Combinatorics and Probability)

調度與(yu) 排序 (Scheduling and Sequencing):

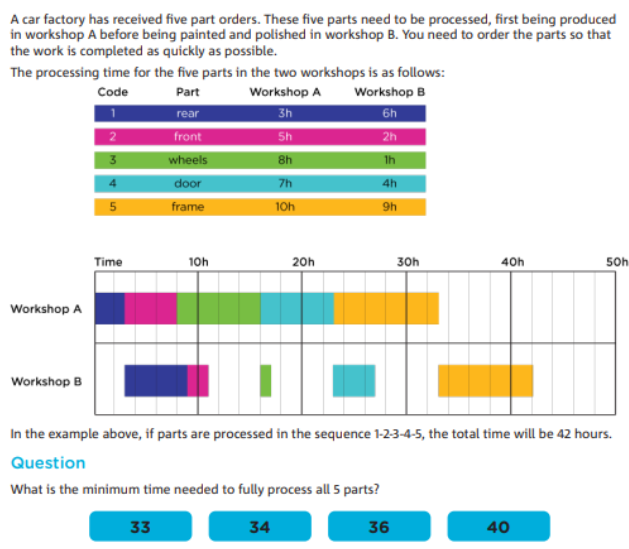
題目要求學生將不同的汽車零件的加工順序進行優(you) 化，以確保總加工時間最短。這是一個(ge) 經典的調度問題，屬於(yu) 組合數學中的排序與(yu) 優(you) 化問題。

並行處理與(yu) 資源優(you) 化(Parallel Processing and Resource Optimization):

由於(yu) 兩(liang) 個(ge) 車間需要並行處理不同的任務，學生需要考慮如何安排這些任務，以最小化整個(ge) 過程的總時間。這涉及到資源的合理分配與(yu) 利用，以實現時間的最小化。

排列組合(Permutations and Combinations):

學生需要考慮不同的排列組合，以確定哪一種排列方式能夠使加工時間最短。

06、機器學習(xi) 基礎(Basics of Machine Learning)

狀態機與(yu) 狀態轉換(State Machines and State Transitions):

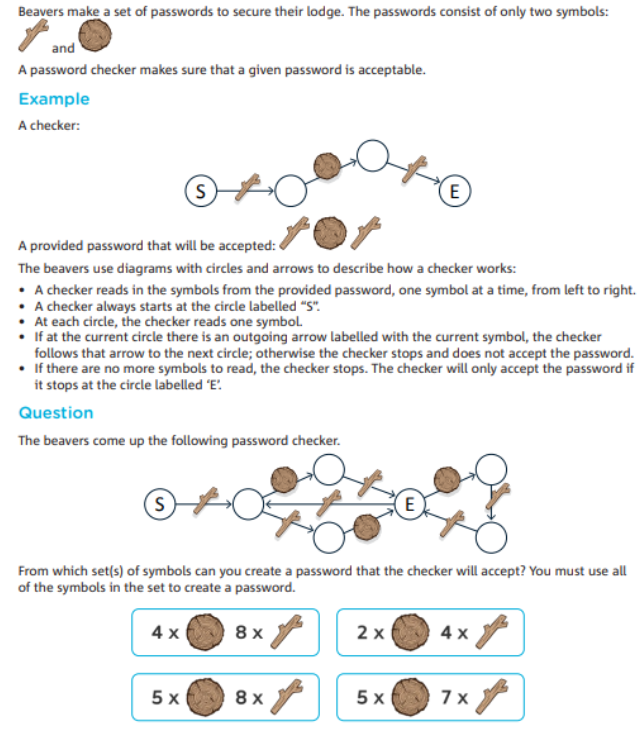
題目中的密碼檢查器實際上是一個(ge) 有限狀態機 (Finite State Machine, FSM)，根據輸入符號的不同進行狀態轉換。學生需要理解狀態機的工作原理，特別是在不同輸入情況下如何進行狀態轉換，以及如何判斷最終狀態。

路徑識別與(yu) 決(jue) 策樹(Path Recognition and Decision Trees):

題目中不同的路徑代表了不同的符號序列，類似於(yu) 決(jue) 策樹中的不同路徑。學生需要識別哪些路徑能夠通過狀態機並最終接受密碼，這與(yu) 機器學習(xi) 中的路徑選擇和決(jue) 策過程類似。

符號序列的生成與(yu) 驗證 (Sequence Generation and Validation):

學生需要生成符號序列並驗證它們(men) 是否能夠被狀態機接受，這類似於(yu) 在機器學習(xi) 中生成並驗證特征序列的過程，以確保最終結果符合期望。

07、密碼學與(yu) 信息安全(Cryptography and Information Security)

算法的抽象與(yu) 建模 (Abstraction and Modeling of Algorithms):

題目涉及到如何有效地排列和調度零件的加工順序，這是一個(ge) 優(you) 化問題。在密碼學中，優(you) 化算法用於(yu) 加密過程的效率提升。通過對問題的抽象和建模，可以找到最佳的處理順序。

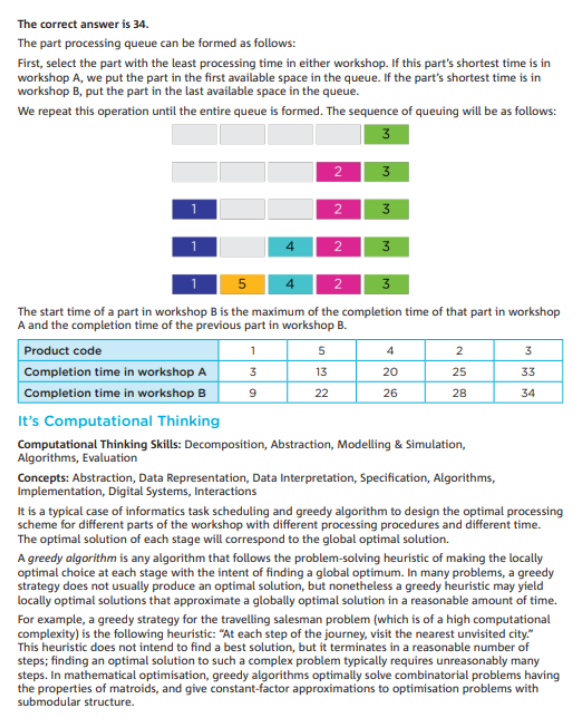
貪心算法 (Greedy Algorithm):

題目中使用了貪心算法來安排零件的加工順序，確保每一步選擇都朝著最小化總時間的方向前進。貪心算法在密碼學中常用於(yu) 簡化計算過程和快速找到次優(you) 解。

數據表示與(yu) 處理 (Data Representation and Processing):

數據表示和處理的方式在信息安全中非常重要，尤其是在優(you) 化算法中。如何有效地表示和處理時間數據，決(jue) 定了最終結果的準確性和有效性。

總結

在Bebras競賽Year 11-13級別的挑戰中，每一個(ge) 考點都是對你智力的極限挑戰，而PGA的課程將幫助你一步步征服這些挑戰。無論是高級算法、圖論，還是機器學習(xi) 和密碼學，我們(men) 將帶你深入淺出地掌握每一個(ge) 知識點，讓你在競賽中遊刃有餘(yu) ，輕鬆取勝。加入PGA課程，踏上這段充滿挑戰與(yu) 樂(le) 趣的競賽之旅，讓你的計算思維和問題解決(jue) 能力達到新的高度！