2023年袋鼠數學思維挑戰活動真題解析（2）

在前幾天的文章《袋鼠數學思維挑戰活動》中，我選擇了袋鼠數學三個(ge) LEVEL共9道代表性的題目。本文將給出這9道題的解答並做一些點評。

袋鼠數學每套題都有不同分值的題目，按題目順序，分值依次是3,4,5分（具體(ti) 分值請參考《袋鼠數學思維挑戰活動》文中的介紹）。隨著分值的增加，題目難度也相應地有所提升。通過每個(ge) LEVEL的3道不同分值的題目的解答，我們(men) 可以體(ti) 會(hui) 其中的難度變化。再換個(ge) 觀察角度，通過比較不同LEVEL的同分值題目的解答，我們(men) 還可以體(ti) 會(hui) 推理的複雜性怎樣隨著年級的增加而增長。

下麵我們(men) 就來具體(ti) 看一下這些題目的解答吧。

LEVEL A

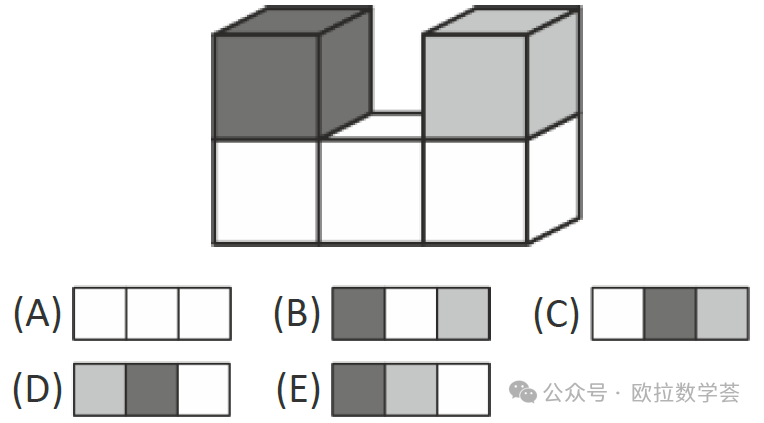
1. 下圖是從(cong) 正麵觀察5個(ge) 立方體(ti) 看到的樣子。那麽(me) 從(cong) 上方觀察會(hui) 看到什麽(me) 呢？（3分題）

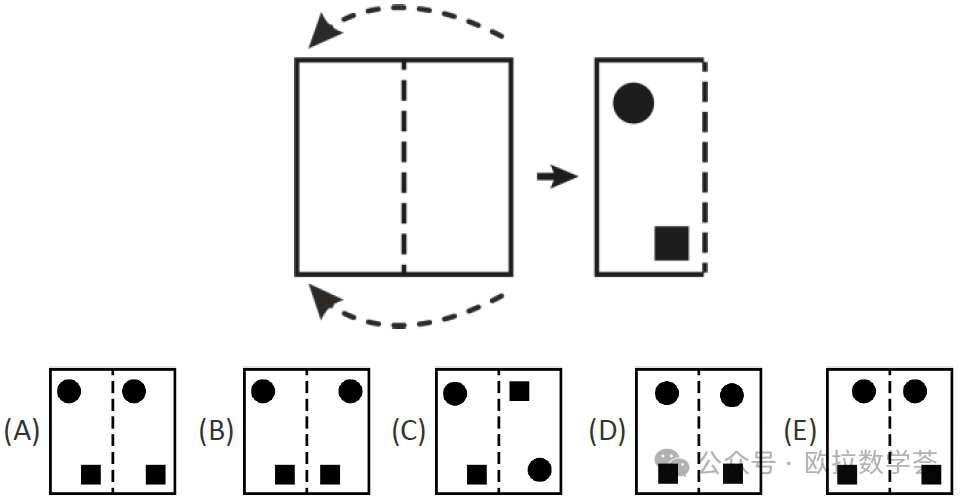
2. 把一張紙對折，然後在紙上打兩(liang) 個(ge) 孔。把這張紙重新展開後會(hui) 是什麽(me) 樣子呢？（4分題）

3. 一個(ge) 池塘裏住著三隻青蛙。每天晚上都會(hui) 有一隻青蛙唱歌，另外兩(liang) 隻青蛙隻是聽歌而不唱歌。在9個(ge) 晚上後，第一隻青蛙唱了2次歌，第二隻青蛙聽了5次歌。第三隻青蛙聽了多少次歌？（5分題）

解答和點評

第1題是圖形觀察題。從(cong) 上方應該看到從(cong) 左到右排列的三個(ge) 正方形，顏色依次是黑、白、灰。所以答案是（B）。

第2題考查圖形的對稱關(guan) 係。在折疊後的紙上打孔，展開後的兩(liang) 個(ge) 孔應該關(guan) 於(yu) 折痕對稱。左半側(ce) 的兩(liang) 個(ge) 孔的位置符合題圖的是A,B,C三個(ge) 選項，其中A和C不符合對稱關(guan) 係。所以答案是（B）。

上麵這兩(liang) 道圖形題跟常識的關(guan) 係非常緊密。一二年級的孩子應該多接觸實物，建立起這些常識觀念，再來做這樣的題目，而不是為(wei) 了解題而解題，生硬地給孩子講解題目。很多優(you) 秀的數學啟蒙遊戲都是以幫助孩子建立這些常識為(wei) 目的而進行設計的。

第3題是推理題。這道題有多種推理方式。在此僅(jin) 介紹其中兩(liang) 種。特別提醒一下，你也許認為(wei) 下麵的推理過程不算太複雜，但這對於(yu) 二年級的小朋友來說已經是很長的邏輯鏈條了。

解法一：對每隻青蛙而言，每個(ge) 晚上要麽(me) 在唱歌，要麽(me) 在聽歌。已知第二隻青蛙聽了5次歌，所以它唱了9-5=4次歌。而第一隻青蛙唱了2次歌，所以第三隻青蛙唱了9-2-4=3次歌。從(cong) 而，第三隻青蛙聽了9-3=6次歌。

解法二：當一隻青蛙在聽歌時，那個(ge) 晚上一定是另兩(liang) 隻青蛙中的一隻在唱歌。已知第二隻青蛙聽了5次歌，所以第一和第三隻青蛙一共唱了5次歌，即第三隻青蛙唱了5-2=3次歌。所以第三隻青蛙聽了9-3=6次歌。LEVEL B

1. 瑪麗(li) 按照下圖所示的時間安排開和關(guan) 三盞燈。有多少分鍾是恰好有兩(liang) 盞燈開著的？（3分題）

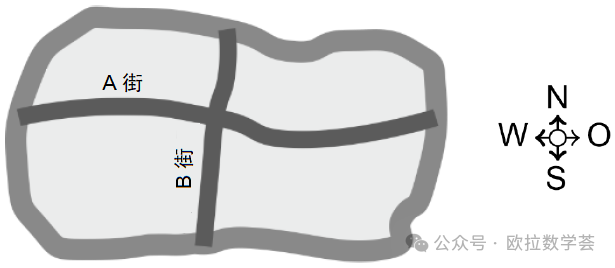
2. 如下圖，A街的北側(ce) 有7棟房子，B街的東(dong) 側(ce) 有8棟房子，A街的南側(ce) 有5棟房子。請問B街的西側(ce) 有多少棟房子？（4分題）

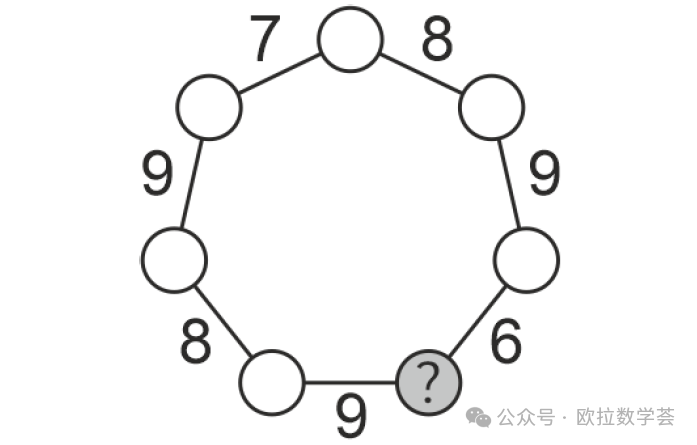
3. 老師在下圖的圓圈內(nei) 分別填入從(cong) 1到7的數，每個(ge) 圓圈內(nei) 填一個(ge) 數。相鄰兩(liang) 個(ge) 圓圈內(nei) 的數的和寫(xie) 在兩(liang) 個(ge) 圓圈的連線旁邊，如圖所示。打問號的圓圈內(nei) 填的是哪個(ge) 數？（5分題）

解答和點評

第1題是圖表觀察題，隻需要數一下有多少個(ge) 分鍾是恰好出現了兩(liang) 條線段的。從(cong) 圖中可以看出，第2, 4, 5, 6, 7, 9, 11, 12分鍾都符合要求，一共是8分鍾。

第2題是推理題。通過觀察街道圖，A街的北側(ce) 和南側(ce) 的房子加起來就是圖中所示的區域內(nei) 的所有房子。所以這個(ge) 區域內(nei) 一共有5+7=12棟房子。類似地，B街東(dong) 側(ce) 和西側(ce) 的房子加起來也是區域內(nei) 的所有房子。而已知B街東(dong) 側(ce) 有8棟房子，所以B街西側(ce) 有12-8=4棟房子。

第3題仍然是推理題，並且與(yu) 第2題一樣，都需要結合對圖的觀察來展開推理。當推理過程揭曉後，也許你會(hui) 感覺非常簡單；但剛讀完題和看完圖時，你的第一感覺很可能是——無從(cong) 下手。

如果你僅(jin) 僅(jin) 根據和的關(guan) 係去嚐試填出這7個(ge) 圓圈內(nei) 的數，除非有中彩票大獎的運氣，否則必定要經曆很多次失敗。而對大多數人來說，四五次失敗就足以把他們(men) 打擊到放棄努力了。

事實上，這個(ge) 題目並沒有要求確定每個(ge) 圓圈內(nei) 的數，而隻要求確定其中一個(ge) 特定位置上的數。這道題的設計，是希望引導孩子從(cong) 單個(ge) 的和關(guan) 係的推導提升到整體(ti) 的和關(guan) 係的分析——前者是我們(men) 通常能“自然而然”地想到的辦法，而後者則需要通過係統性的訓練才能建立起來。再多延伸說一句，“全局性推理”是數學方法論中一個(ge) 重要且普遍應用的思維模式，不僅(jin) 對於(yu) 數學問題，而且對我們(men) 思考不同領域內(nei) 的問題都大有裨益。

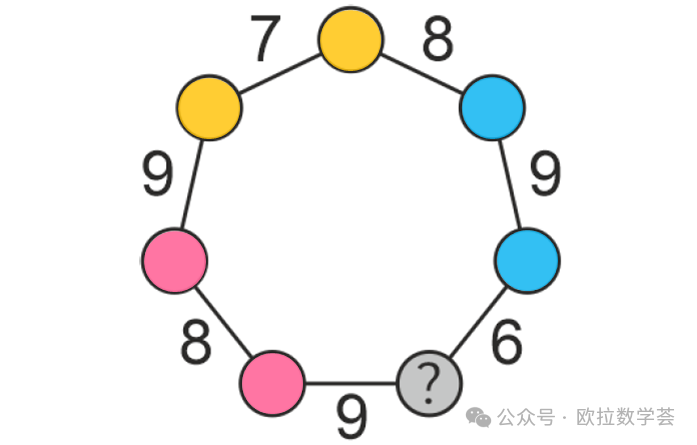
在上圖中，我們(men) 同時考慮三個(ge) 和關(guan) 係。兩(liang) 個(ge) 紅色圓圈內(nei) 的數之和是8，兩(liang) 個(ge) 黃色圓圈內(nei) 的數之和是7，兩(liang) 個(ge) 藍色圓圈內(nei) 的數之和是9。所以三組共6個(ge) 數的和是8+7+9=24。而從(cong) 1到7這7個(ge) 數的和是1+2+···+7=28。所以剩下的那個(ge) 數應該是28-24=4，也是打問號的圓圈內(nei) 必須要填的數。雖然這三組共6個(ge) 數應該填的位置我們(men) 一個(ge) 都沒有確定，但我們(men) 可以肯定（如果要滿足題目的條件）它們(men) 的和一定是24，進而推斷打問號的圓圈內(nei) 必須填4。

盡管上麵的做法隻是填出了一個(ge) 特定圓圈內(nei) 的數，但從(cong) 這個(ge) 數出發，我們(men) 就能把其他圓圈內(nei) 的數逐個(ge) 填出來。

一般地說，隻要能確定其中任意一個(ge) 圓圈內(nei) 的數，就能把所有圓圈內(nei) 的數都填出來。這裏我再多提一個(ge) 問題：如果我們(men) 要求先確定正上方的圓圈（即和數7右邊的黃色圓圈）內(nei) 的數，你有沒有什麽(me) 巧妙的辦法？LEVEL C

1. 如下圖所示，圓柱形塔有一個(ge) 梯子從(cong) 底部直通到頂部。梯子的每個(ge) 梯級都一樣高。圖中可以看到9個(ge) 梯級。還有多少個(ge) 梯級是看不見的？（3分題）

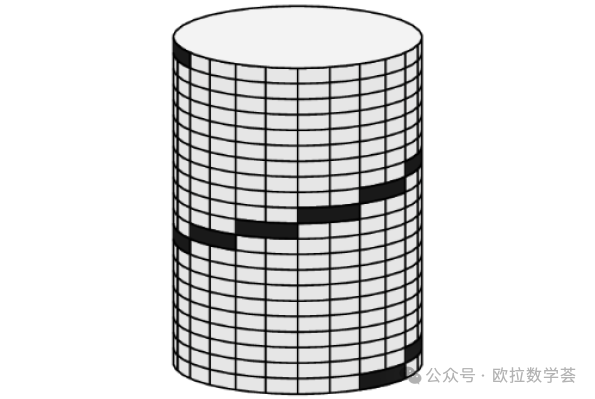
2. 一個(ge) 露台上鋪著三種不同大小的正方形瓷磚。最小的瓷磚周長為(wei) 80厘米。如圖所示，一條蛇沿著瓷磚的邊緣躺在露台上。這條蛇的長度是多少厘米？（4分題）

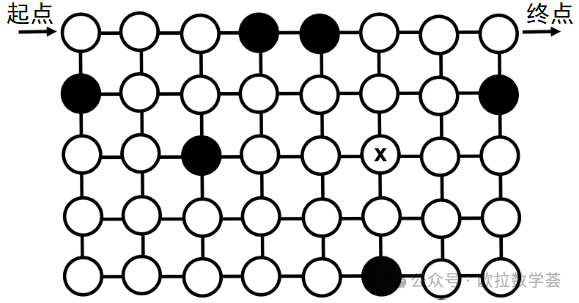
3. 莫妮卡想在迷宮裏找到一條從(cong) 左上方的圓圈開始，到右上方的圓圈結束的路徑。她隻能水平或垂直移動到相鄰的圓圈，並且隻能移動到白色圓圈。此外，每個(ge) 白色圓圈都要恰好經過一次。當她到達標有X的圓圈時，下一步是向哪個(ge) 方向移動？（5分題）

解答和點評

第1題是圖形觀察題。通過觀察梯子，可以發現塔身的每一行都剛好有一個(ge) 梯級。所以梯級的總數就是塔身的行數。直接數出塔身共有21行（建議至少數兩(liang) 遍，以確保沒有數錯），所以有21-9=12個(ge) 梯級是看不見的。

第2題是圖形計算題。根據三種正方形瓷磚的擺放關(guan) 係，可以推出從(cong) 小到大的邊長分別是20,40,60厘米（具體(ti) 推導過程不在這裏贅述）。把蛇身分成12段，然後再把各段長度相加，可得蛇的長度是20×5+40×5+60×2=420厘米。

第3題的圖的設計非常巧妙，用“獨具匠心”來形容也不為(wei) 過。滿足題目要求的路徑事實上隻有一條，而為(wei) 了確定這條路徑，我們(men) 需要從(cong) 起點開始一步一步地、像掃雷一樣確定下一步應該到達哪個(ge) 圓圈的位置。要在限時的考試中通過準確的推理把這條路徑找出來，對孩子的分析能力是很大的挑戰。不過，我並不認為(wei) 這道題的意義(yi) 僅(jin) 僅(jin) 是訓練我們(men) 在短時間內(nei) （例如5分鍾）完成整個(ge) 推導過程。如果你能用20或30分鍾完成，這仍然是非常有益的訓練過程。完成時間的長短固然反映了能力的高低，但無論時間多長，訓練的作用都是一樣的。

每個(ge) LEVEL的5分題都是難度最高的題目。從(cong) 這三道5分題的解答中，我們(men) 也可以觀察到孩子的分析和推理能力的構建是怎樣逐步展開和推進的。