史上首次 AI超越人類奧賽金牌得主！

就在剛剛，首位超越人類數學奧賽金牌得主的AI誕生了！劍橋大學等機構的研究者發現，結合「吳方法」的DeepMind數學模型AlphaGeometry，在解決(jue) 奧數題時直接秒殺了人類IMO金牌得主，30道幾何題中做對了27道。

首位超越國際奧林匹克競賽金牌得主的AI，剛剛誕生了！

印度理工學院海得拉巴分校、圖賓根AI中心、劍橋大學的研究者發現——

通過「吳方法」，可以讓AI變成和人類數學奧賽銀牌得主同樣的水平，而「AI數學大師」AlphaGeometry，則直接超越了IMO金牌得主。

吳方法，是吳文俊在1970年代提出的開創性算法。

經過改進後，它變得非常強大，可以解決(jue) 國際數學奧林匹克競賽30個(ge) 問題中的27個(ge) ！直接秒殺人類。

相比之下，之前的AlphaGeometry，僅(jin) 能解決(jue) 25個(ge) 。

論文地址：https://arxiv.org/abs/2404.06405

項目地址：https://huggingface.co/datasets/bethgelab/simplegeometry

之前曾有人估計，到2026年代，AI才能達到IMO人類金牌得主的水平。而如今，這個(ge) 時間表再次被打破了。

AI做IMO奧數題，有新SOTA了

證明幾何定理是視覺推理的重要表現，它融合了直覺和邏輯思維。

因此，自動化證明奧林匹克級別的幾何題目，代表著人類級自動推理的一個(ge) 重要裏程碑。

此前推出的AlphaGeometry，是一個(ge) 通過1億(yi) 個(ge) 合成樣本訓練的神經符號模型，代表了一個(ge) 重大的突破。

論文地址：https://www.nature.com/articles/s41586-023-06747-5

它成功解決(jue) 了國際數學奧林匹克（IMO）30個(ge) 問題中的25個(ge) ，而傳(chuan) 統的基於(yu) 吳方法的係統，僅(jin) 能解決(jue) 10個(ge) 。

但這一次，研究者們(men) 重新評估了AlphaGeometry引入的IMO-AG-30挑戰，有了新的發現——

吳方法異常強大！

僅(jin) 靠吳方法，就能解決(jue) 15個(ge) 問題，其中一些問題是靠其他方法根本無法解決(jue) 的。

而這就帶來了兩(liang) 個(ge) 關(guan) 鍵發現：

1. 通過將「吳方法」和經典的演繹數據庫（DD）以及角度、比率和距離追蹤（AR）的合成方法相結合，僅(jin) 使用一台配備CPU的筆記本，在每個(ge) 問題的5分鍾限時內(nei) ，就能解決(jue) 30個(ge) 問題中的21個(ge) 。

這種經典組合方法（Wu&DD+AR）僅(jin) 比AlphaGeometry少解決(jue) 了4個(ge) 問題，並建立了第一個(ge) 完全基於(yu) 符號的基準，其性能足以與(yu) 國際數學奧林匹克（IMO）銀牌得主媲美。

2. 吳方法還解決(jue) 了AlphaGeometry未能解決(jue) 的5個(ge) 問題中的2個(ge) 。

因此，現在IMO-AG-30有新的SOTA了！

通過將AlphaGeometry與(yu) 吳方法結合產(chan) 生的新AI，直接解決(jue) 了30個(ge) 問題中的27個(ge) ，一舉(ju) 超越IMO金牌得主，成為(wei) 世上首個(ge) 達此成就的AI。

歐氏幾何，AI推理能力的試金石

如何測試AI的推理能力強不強？歐幾裏得幾何就是一個(ge) 很好的標準。

因為(wei) ，歐幾裏得幾何已經被有限地公理化了，而且這麽(me) 多年來，有許多非常適合自動定理證明的歐幾裏得幾何證明係統被提了出來。

此外證明的搜索可以通過圖形表示、概率驗證，或是使用人類設計的啟發式方法，來對角度、麵積和距離進行大量推理引導。

國際數學奧林匹克中，這些方法被參賽者戲稱為(wei) 「三角破解」和「重心破解」。

還有一件有趣的事，就是這個(ge) 領域的缺陷——它需要定義(yi) 特定的證明係統來指定問題，缺乏訓練數據，問題時常涉及複雜的退化情況。

這些困難非常棘手，由此坊間有這樣一句戲言——「幾何問題永遠不會(hui) 解決(jue) 退化問題。」

在幾何自動推理領域，可以將方法分為(wei) 代數方法和合成方法。

演繹數據庫（DD）這個(ge) 合成方法就頗受關(guan) 注。

它會(hui) 模仿人類的證明技巧，通過將定理證明視為(wei) 依據一組幾何公理進行的逐步搜索問題，從(cong) 而生成易於(yu) 理解的證明。

比如，DD會(hui) 采用一組固定的、由專(zhuan) 家策劃的幾何規則，這些規則會(hui) 不斷地應用到初始的幾何配置上，直至係統達到一個(ge) 狀態，即用現有規則無法推導出新的事實為(wei) 止。

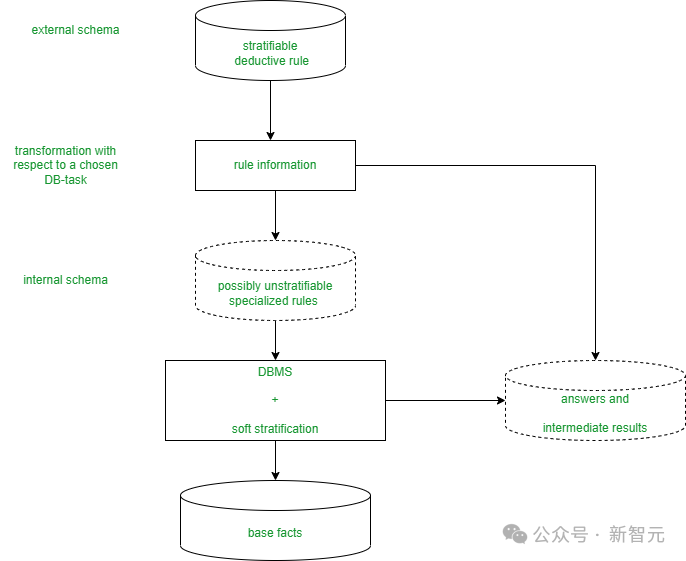
而神經符號證明器AlphaGeometry在這一領域取得了突破性的進展。

在DD的基礎上，它增加了新的規則，用於(yu) 進行角度、比率和距離的追蹤（AR），並通過大模型（DD+AR+LLM-構造）提出的構建方法，進一步增強了由此生成的符號引擎。該模型是基於(yu) 1億(yi) 個(ge) 合成證明訓練的。

而吳方法和Gröbner基方法之類的代數方法，能夠將幾何假設，轉換成多項式係統，來驗證結論。

這些方法已被證實，能夠有效處理廣泛的幾何問題。

其中，對於(yu) 所有假設和結論都能用代數方程表示的問題，吳方法都能處理，並且還能自動產(chan) 生非退化條件。

而這就表明，吳方法不僅(jin) 適用於(yu) 平麵幾何問題，也適用於(yu) 固體(ti) 和更高維的幾何問題。

5秒解決(jue) 14個(ge) 問題

今年1月，穀歌DeepMind團隊同時推出了新的基準測試IMO-AG-30。

這是團隊從(cong) 2000年至2022年間競賽題中，篩選出30道經典幾何問題組成的測試集，目的是為(wei) 了展示AlphaGeometry的性能。

基準中，問題的解決(jue) 數量與(yu) IMO選手的平均解題數量相對應。

如下圖，灰色水平線所示，銅牌、銀牌和金牌得主平均分別解決(jue) 了19.3個(ge) 、22.9個(ge) 和25.9個(ge) 問題。

所有參賽者平均解題數為(wei) 15.2。

IMO-AG-30收集的具體(ti) 問題集在圖1（B）的左列中有所列出。

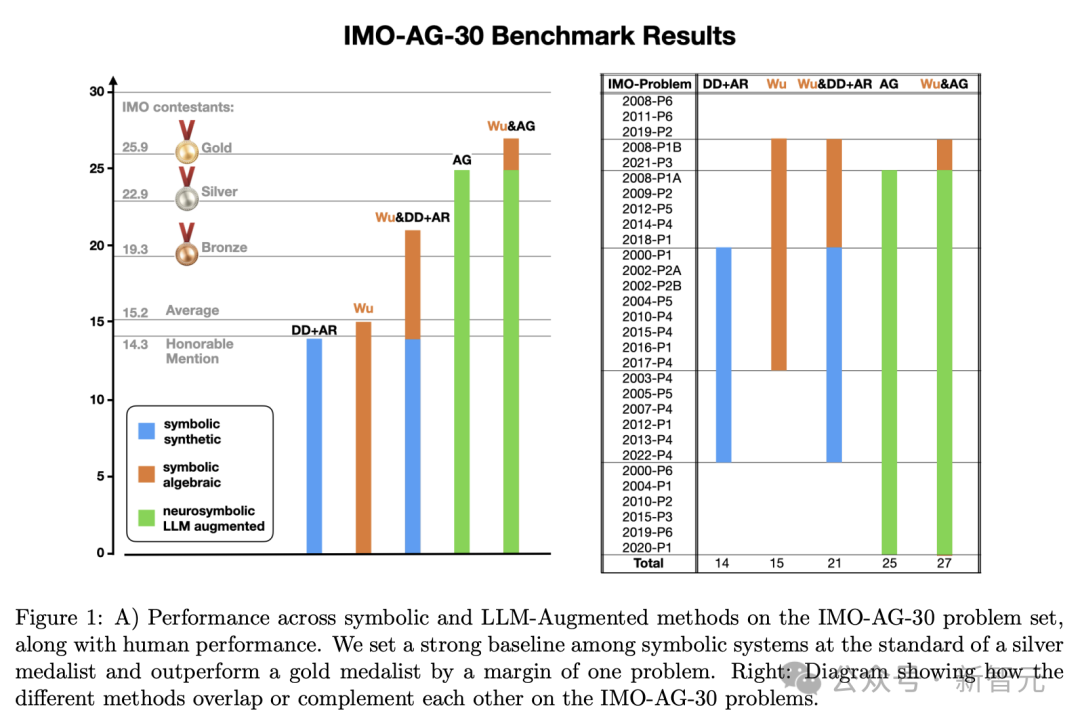
（A）在IMO-AG-30問題集上，符號係統和增強型大模型（LLM-Augmented）的表現，以及與(yu) 人類表現的對比

（B）展示了不同方法在解決(jue) IMO-AG-30問題集時的情況

實驗

研究人員根據Trinh等人提供的基線和數據集，使用IMO-AG-30基準進行性能評估。

他們(men) 通過JGEX軟件手動將IMO-AG-30問題轉換成兼容格式，並重新實現了吳方法。

同時，研究者也從(cong) AlphaGeometry代碼庫中成功重現了必要的DD+AR基線。

經過手動驗證了自己翻譯的幾個(ge) 問題，團隊確認JGEX生成的假設和結論方程是正確的。

吳方法解決(jue) 了AlphaGeometry未能解決(jue) 的兩(liang) 個(ge) 問題，方案插圖如下所示。

2008-P1B（JGEX）：

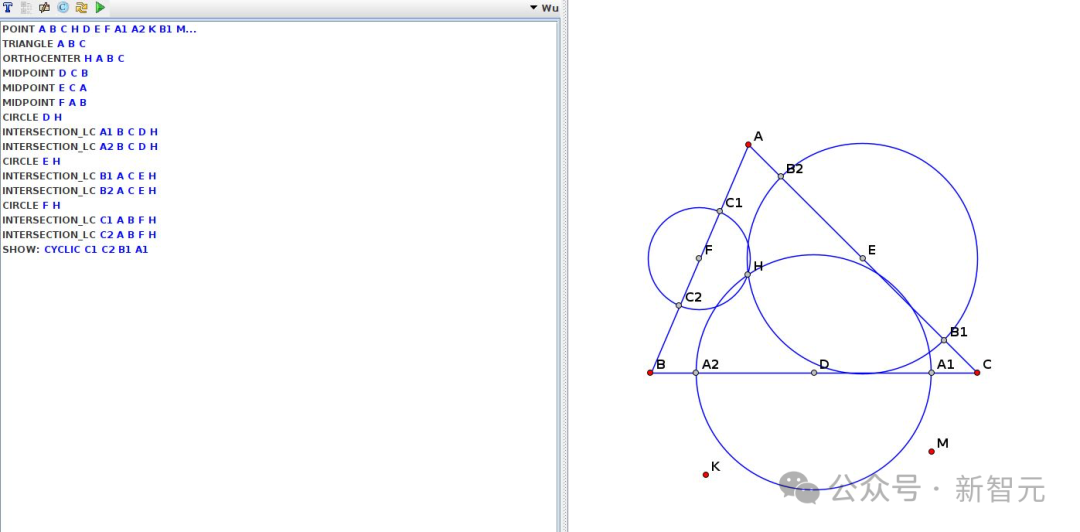
生成的答案：

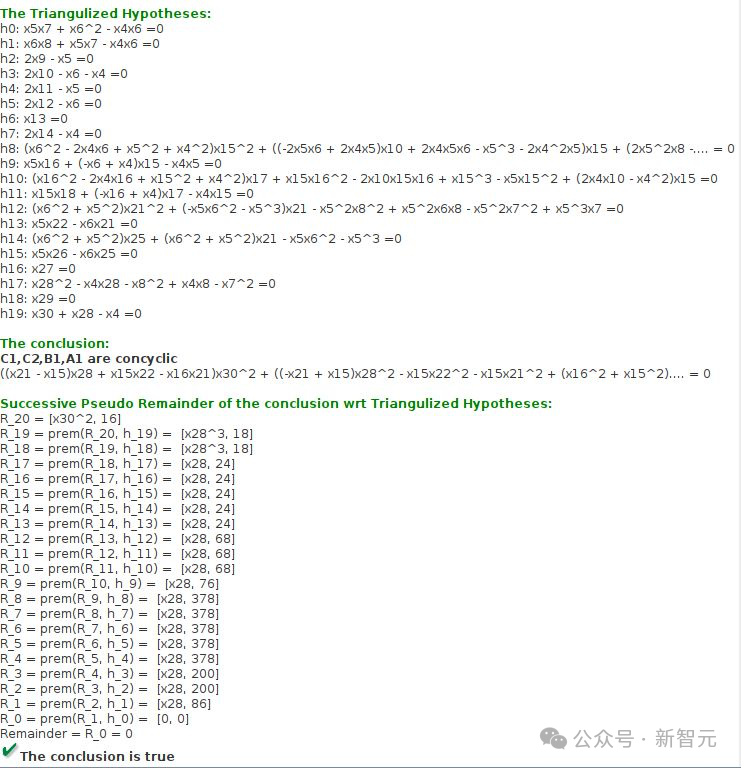
2021-P3（JGEX）：

生成的答案：

結果

研究結果與(yu) 的先前結果，已經在圖1中進行了展示。

圖1（A）比較了解決(jue) 問題的數量，圖1（B）展示了各種方法解決(jue) 的具體(ti) 問題，以此可視化不同方法之間的重疊或互補性。

具體(ti) 來說，研究人員將吳方法與(yu) DD+AR結合，創建了一個(ge) 新的符號性能基準（Wu&DD+AR），該基準比所有傳(chuan) 統方法多解決(jue) 了6個(ge) 問題。

這種組合解決(jue) 了IMO-AG-30問題中的21個(ge) ，與(yu) 圖2中未經微調（僅(jin) FT-9M）的AlphaGeometry的表現相匹配。

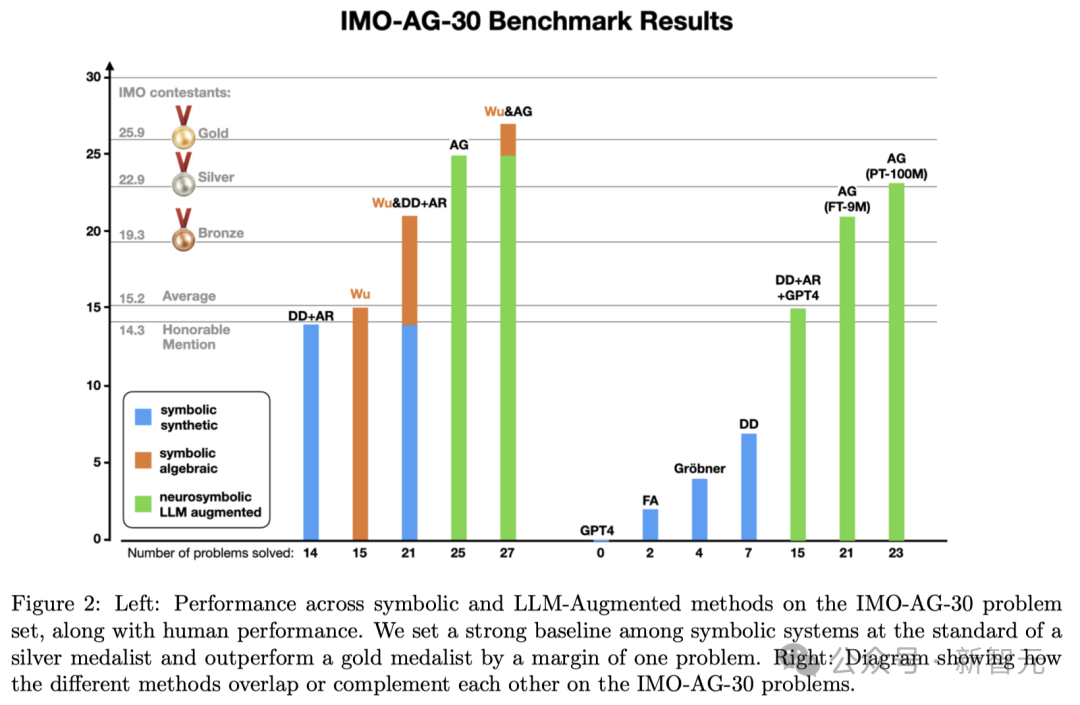（A）展示了在IMO-AG-30問題集上，符號方法和LLM增強（LLM-Augmented）方法的表現，以及與(yu) 人類表現的對比

（B）展示了不同方法在IMO-AG-30問題上的表現

吳方法在非常低的計算需求下實現了這一表現。

在一台裝有AMD Ryzen 7 5800H處理器和16 GB RAM的筆記本上，研究人員在5秒內(nei) 解決(jue) 了15個(ge) 問題中的14個(ge) ，其中一個(ge) 問題（2015 P4）需要耗時3分鍾。

在實驗中，吳方法要麽(me) 幾乎立即解決(jue) 問題，要麽(me) 在5分鍾內(nei) 使筆記本內(nei) 存耗盡。

值得一提的是，研究者通過吳方法解決(jue) 的15個(ge) 問題中的2個(ge) （2021 P3, 2008 P1B），原本是AlphaGeometry難以解決(jue) 的5個(ge) 問題之中的2個(ge) 。

因此，通過簡單地將Wu的方法與(yu) AlphaGeometry結合，實現了在IMO-AG-30基準上解決(jue) 了27個(ge) 問題，這一成就在圖1的綠色/橙色條形（Wu&AG）中有所展示。

代數方法攻克IMO

代數方法，在自動化幾何推理中解決(jue) IMO幾何問題中，蘊藏著巨大的潛力。

這項研究恰恰印證了這一點，吳方法也從(cong) 過往能夠解決(jue) 10個(ge) 問題，增加到了15個(ge) 問題。

而這些問題中，有幾個(ge) 對於(yu) 目前流行的合成方法，以及增強LLM的方法，也具有非常高的挑戰性。

研究者表示，其設立的符號基線，是首個(ge) 在性能上超越一般IMO參賽者，並接近銀牌水平。

此外，AlphaGeomtery和吳方法結合的係統，也是首個(ge) 在IMO幾何問題上超越人類金牌得主的AI係統。

這一成就證明了，代數方法與(yu) 合成方法在這一領域的互補性。特別是，2008 P1B和2021 P3這兩(liang) 個(ge) 問題目前僅(jin) 有吳方法能解決(jue) ，顯示了代數方法的獨特價(jia) 值。

盡管代數方法以其理論保證而著稱，但之前因速度慢和難以為(wei) 人理解而受到質疑。

而最新的研究觀察顯示，吳方法在多個(ge) 問題上的效率遠超預期，作者認為(wei) 不應僅(jin) 因其無法生成人類可讀的證明而忽視它。

目前，研究還在進行中，受限於(yu) 現有實現的不足，包括結構的限製和性能不佳。

研究者相信，傳(chuan) 統方法有可能超越AlphaGeometry的證明能力，並希望這份研究能促進這一領域經典計算方法軟件的改進。

另一方麵，最新方法取得的顯著成功表明，盡管IMO幾何問題對人類具有挑戰性，但可能並未充分挑戰現代計算求解器的極限。

解題的成功更多依賴於(yu) ，重複使用人定義(yi) 的啟發式方法和有限的構造，而不是深入探索複雜的組合可能性。

這與(yu) 國際象棋殘局的情況類似，其相對較早就被暴力求解器掌握了。

而研究人員希望這份研究，能激勵開發幾何領域自動定理證明器的新基準。