AMC8真題第11期解析-這道題不簡單！

上一期的AMC8真題主要考察了直線方程、圓的麵積、三角形麵積的計算等知識哦。

來看看本期老師帶來的答案解析吧！

第1題A rectangle, with sides parallel to the x-axis and y-axis, has opposite vertices located at (15,3)and (16,5). A line is drawn through points A(0,0) and B(3,1). Another line is drawn through points C(0,10) and D(2,9). How many points on the rectangle lie on at least one of the two lines?

一個(ge) 矩形，其邊平行於(yu) x軸和y軸，其相對的頂點位於(yu) (15,3)和(16,5)。通過點A(0,0)和B(3,1)畫一條直線。另一條線通過點C(0,10)和D(2,9)。矩形上有多少個(ge) 點位於(yu) 兩(liang) 條直線中的至少一條上?  

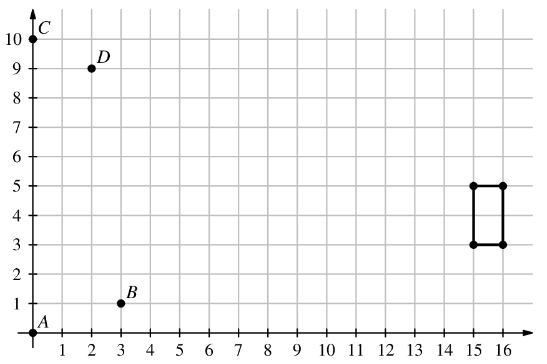
問矩形中有多少個(ge) 點位於(yu) 兩(liang) 條直線中的至少一條上，

我們(men) 可以通過直線方程驗證是否經過（15，3）：

設經過CD的直線為(wei) y=k1x+b1，

將C，D兩(liang) 點代入得

b1=10，

2k1+10=9, k1=-1/2，

所以經過CD的直線方程為(wei) y=-1/2x+10，

x=15時，y=-1/2·15+10=2.5，

因此，CD並不會(hui) 經過矩形。

再來看AB，設y=k2x+b2，

將A，B兩(liang) 點代入得

b2=0,

3k2=1, k2=1/3，

所以經過AB的直線方程為(wei) y=1/3x，

當x=15時，y=1/3·15=5

也就是說，直線AB剛好經過點（15，5）。

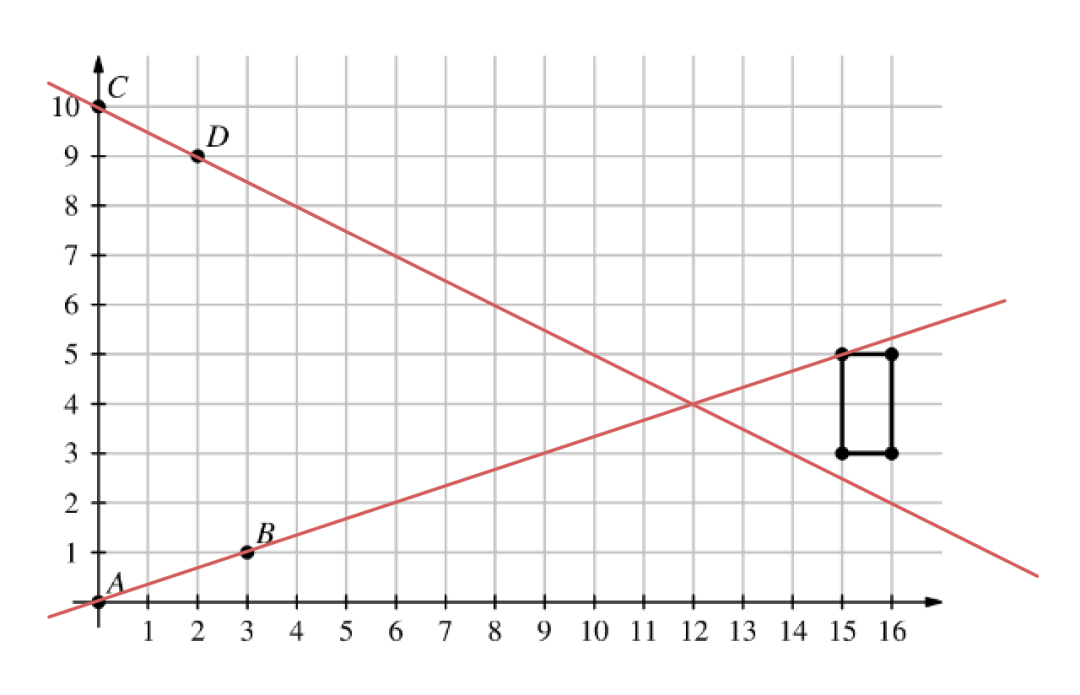
因此，矩形中隻有一個(ge) 點位於(yu) 兩(liang) 條直線中的至少一條，即直線AB上。

如下圖所示：

第2題The figure below shows a large white circle with a number of smaller white and shaded circles in its interior. What fraction of the interior of the large white circle is shaded?

下圖顯示了一個(ge) 白色圓圈，在其內(nei) 部有許多較小的白色圓圈和陰影圓圈。問白色大圓的內(nei) 部陰影占多少?  

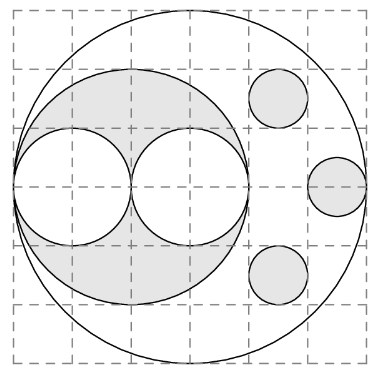
我們(men) 假設每個(ge) 小方格的邊長為(wei) 1，那麽(me) 白色大圓的半徑就是3，

圓的麵積公式：

s=πr²=π·3²=9π

我們(men) 先求最大的陰影圓的陰影部分占了多少麵積，

也就是用最大的陰影⚪的麵積-兩(liang) 個(ge) 白色小⚪的麵積，

即π2²-2·π·1²=4π-2π=2π，

再來計算三個(ge) 小的陰影⚪麵積：

s=3·πr²=3·π0.5²=3·0.25π=0.75π，

所以陰影部分的麵積總共占（2+0.75）π=2.75π=11/4π，

所以陰影占白色大⚪的部分=11/4π÷9π=11/36，

所以白色大⚪內(nei) 部陰影占了11/36。

第3題

Isosceles triangle ABC has equal side lengths AB and BC. In the figures below, segments are drawn parallel to AC so that the shaded portions of

▲ABC have the same area. The heights of the two unshaded portions are 11 and 5 units, respectively. What is the height h of ▲ABC? 等腰三角形ABC的邊長AB和BC相等。在下麵的圖中，線段與(yu) AC平行，因此▲ABC的陰影部分具有相同的麵積。兩(liang) 個(ge) 未遮擋部分的高度分別為(wei) 11和5個(ge) 單位。問▲ABC的高度h是多少?

由圖可知，兩(liang) 個(ge) 三角形為(wei) 全等三角形，所以兩(liang) 個(ge) 三角形麵積相等，

灰色梯形的麵積可以表示為(wei) ：

S▲ABC-(11/h)²·S▲ABC

S▲ABC[1-(11/h)²]

灰色三角形的麵積可以表示為(wei) ：

S▲ABC·[(h-5)/h]²

兩(liang) 個(ge) 陰影麵積相等，即

1-(11/h)²=[(h-5)/h]²

1-121/h²=(h²-10h+25)/h²

h²-121=h²-10h+25)

10h=146

h=14.6

所以▲ABC的高h為(wei) 14.6。

第三道題目不簡單！同學們(men) 需要多多練習(xi) 類似的題型，做到滾瓜爛熟！這樣考場才不會(hui) 腦袋空空，不知所措哦。真題挑戰還在繼續！