劉謙魔術背後約瑟夫問題的計算機求解

約瑟夫問題

劉謙在今年春晚表演的魔術，在本質上就是一個(ge) 【約瑟夫問題】。

約瑟夫問題（有時也稱為(wei) 約瑟夫斯置換）是一個(ge) 出現在計算機科學和數學中的問題。問題的描述為(wei) ：0，1，2···n-1，這個(ge) 數字排成一個(ge) 圓圈，從(cong) 數字開始，每次從(cong) 這個(ge) 圓圈裏刪除第個(ge) 數字（刪除後從(cong) 下一個(ge) 數字開始計數），求出這個(ge) 圓圈裏剩下的最後一個(ge) 數字。

該問題也被稱為(wei) “丟(diu) 手絹問題”。

瑟夫問題在實際生活中有一些潛在的應用，以下是一個(ge) 例子：

l資源分配：在資源有限的情況下，需要按照一定的規則進行分配。例如，有個(ge) 項目需要分配有限的資金，每次分配給排名第的項目，直到資金分配完。這可以類似於(yu) 約瑟夫問題中的數字刪除過程。

l排隊係統：在排隊場景中，類似於(yu) 約瑟夫問題，可以按照一定的規則（如每隔個(ge) 人）讓一部分人先得到服務。

l數據處理：在數據處理中，可能需要按照特定的順序或條件刪除或處理數據元素，這可以通過類似約瑟夫問題的方法來實現。

這些隻是一些可能的應用示例，實際上，約瑟夫問題的思想可以在各種領域中找到潛在的應用。

約瑟夫問題的圖解法

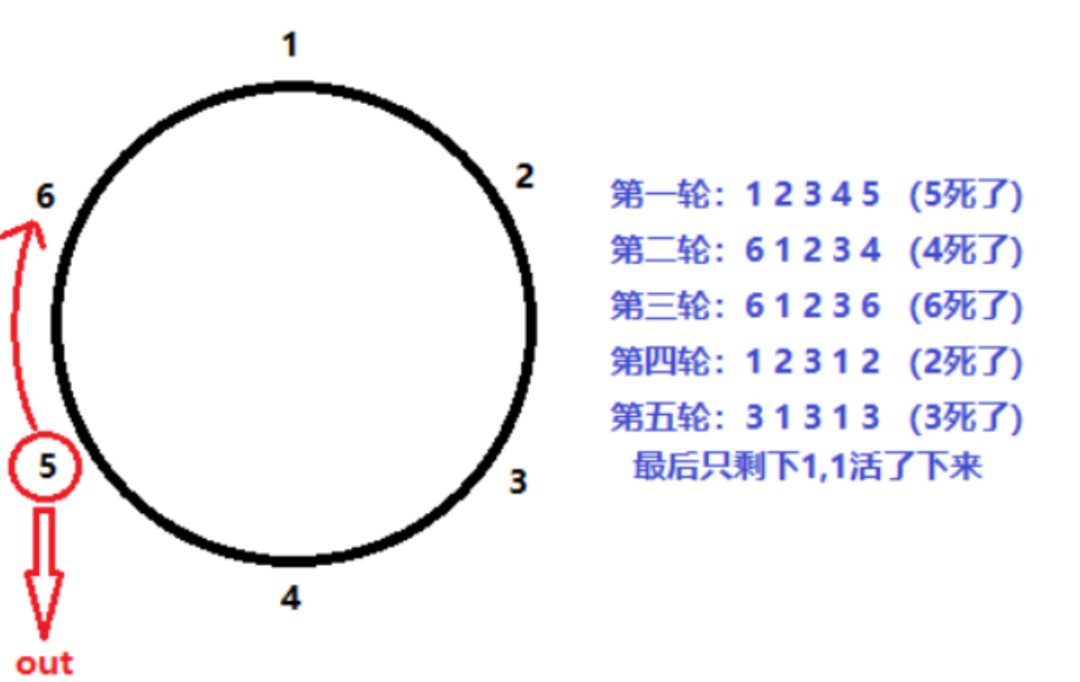
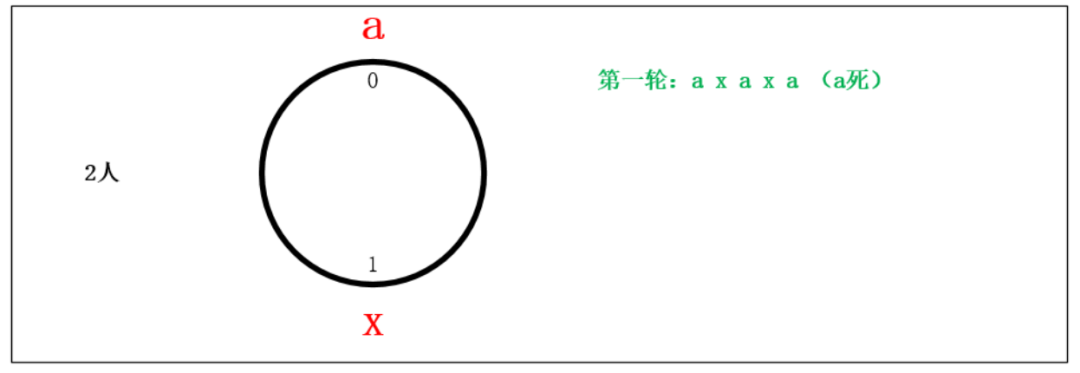
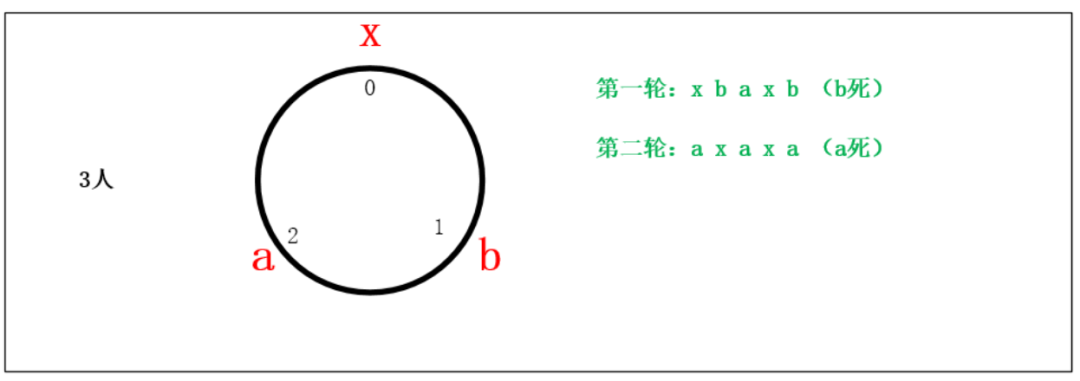
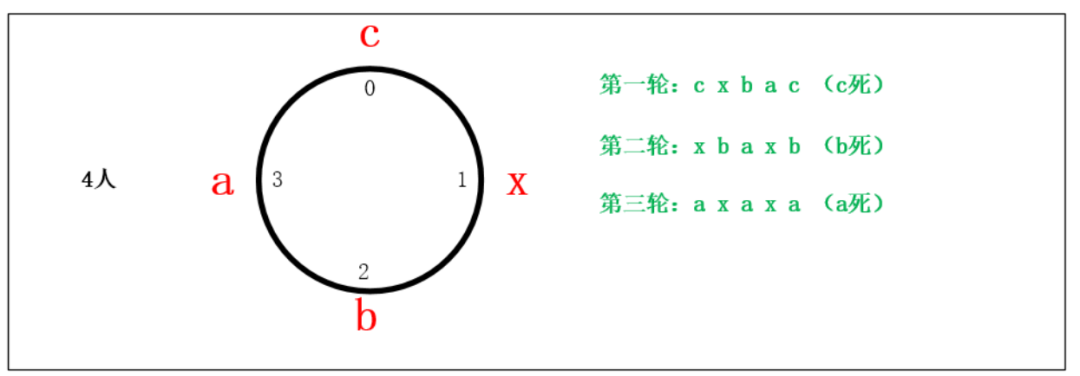
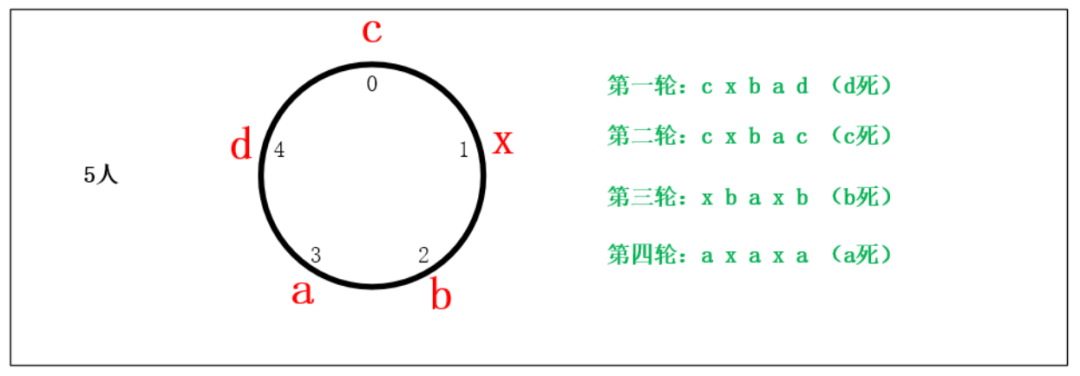
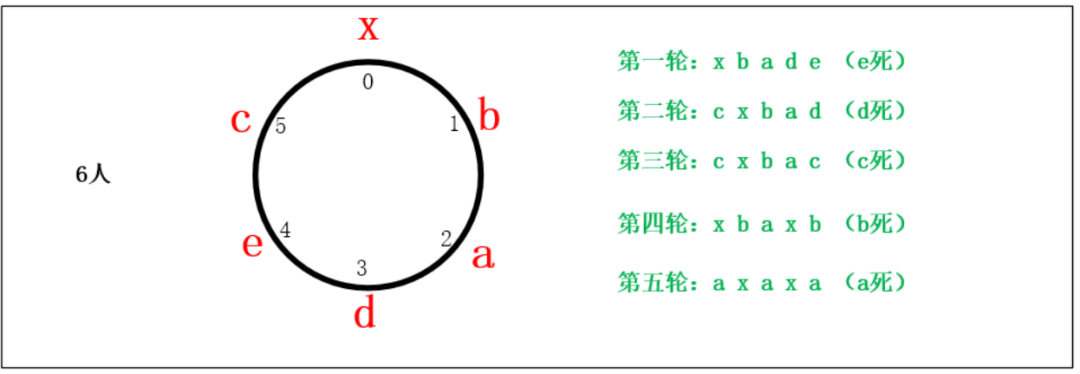
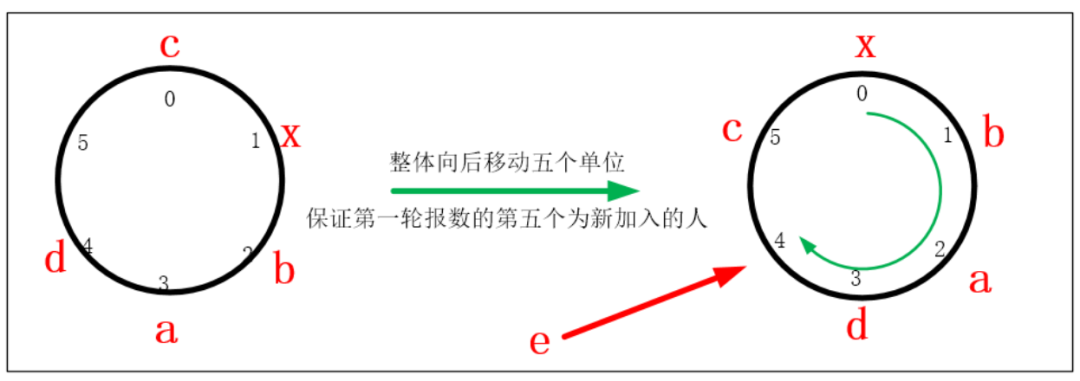
約瑟夫問題的計算機編程  

（1）C語言編程

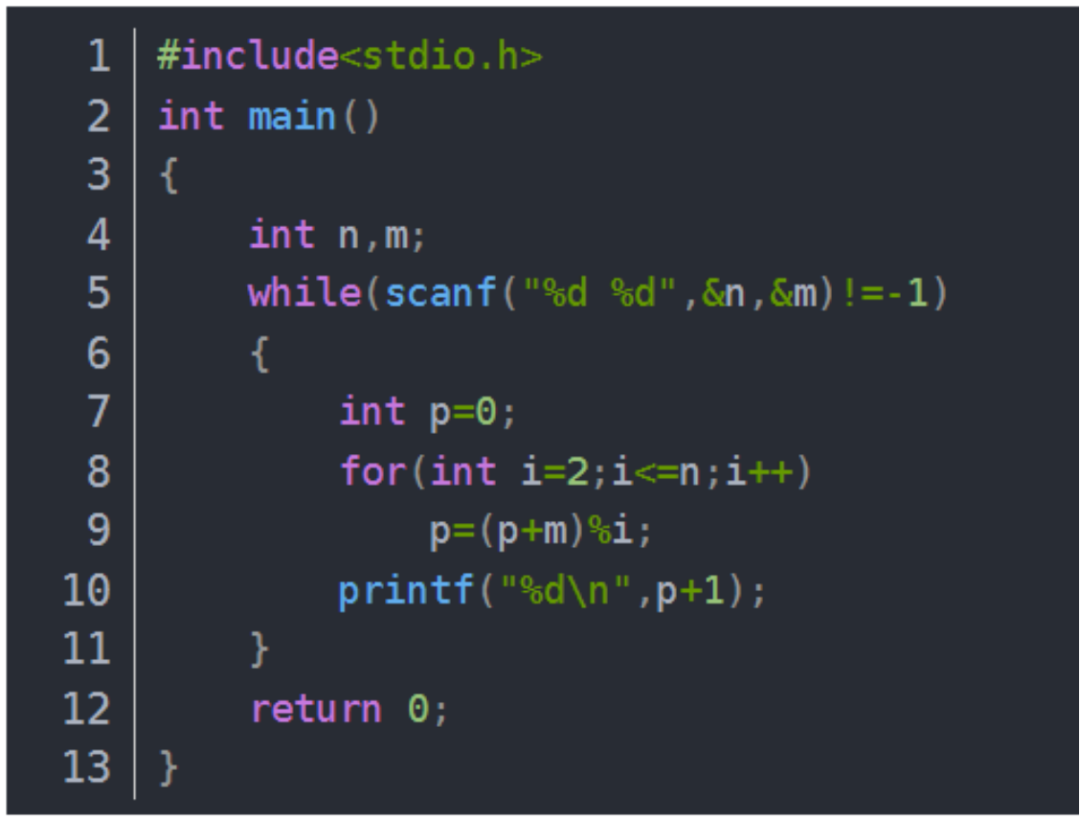
（2）Python語言編程

我們(men) 可以通過創建一個(ge) 列表，並利用pop函數模擬人們(men) 的排列順序，從(cong) 而解決(jue) 約瑟夫問題。以下是一個(ge) 用 Python 解決(jue) 約瑟夫問題的示例代碼：

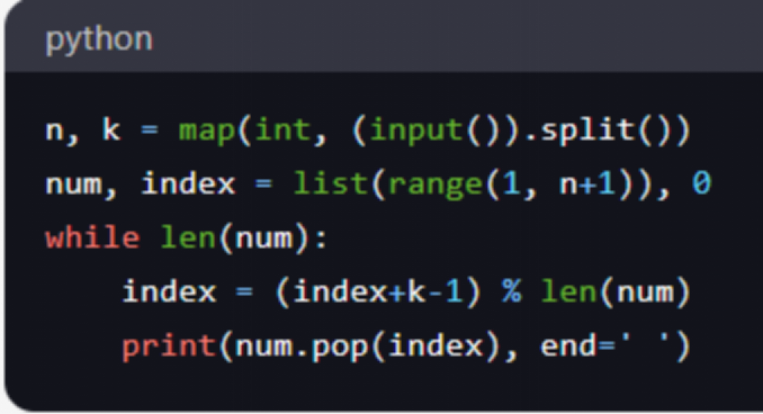
在這個(ge) 示例中，我們(men) 首先定義(yi) 了兩(liang) 個(ge) 變量n和k，分別表示總人數和報數步長。然後，我們(men) 創建一個(ge) 包含所有人編號的列表num，並初始化索引index為(wei) 0。接下來，我們(men) 使用一個(ge) while循環來模擬人們(men) 的排列順序。在每次循環中，我們(men) 計算下一個(ge) 要出圈的人的索引index，然後使用pop函數將此人從(cong) 列表中移除，並輸出其編號。最後，我們(men) 使用split函數將輸入的兩(liang) 個(ge) 整數進行分割，並將它們(men) 轉換為(wei) 整數類型，分別賦值給n和k。

我們(men) 可以從(cong) 以下幾個(ge) 方麵對該程序進行優(you) 化：

l算法優(you) 化：我們(men) 可以嚐試使用其他算法來解決(jue) 約瑟夫問題，例如使用遞歸或動態規劃，這可能會(hui) 使代碼更簡潔和高效。

l數據結構優(you) 化：我們(men) 可以嚐試使用不同的數據結構來存儲(chu) 和操作數字，例如使用列表或隊列，以提高代碼的執行效率。

l循環優(you) 化：我們(men) 可以嚐試使用更有效的循環方式，例如使用for循環或while循環的不同變體(ti) ，以提高代碼的執行效率。

請注意，這些優(you) 化方法可能會(hui) 對代碼的可讀性和可維護性產(chan) 生一定的影響，因此在進行優(you) 化時，需要在效率和可讀性之間進行權衡。

約瑟夫問題的生活案例  

在現實生活中，約瑟夫問題可以有很多不同的應用場景，例如在一個(ge) 公司或團隊中，確定一個(ge) 合適的人選來承擔某項任務或擔任某個(ge) 職位；或者在一個(ge) 項目中，確定一個(ge) 合適的時間點來進行某個(ge) 重要的決(jue) 策或行動。

例如，一個(ge) 公司有10個(ge) 員工，需要選出一個(ge) 人來負責一個(ge) 重要的項目。公司可以采用約瑟夫問題的解決(jue) 方法，確定一個(ge) 數值（步長），表示每次跳過的人數，然後從(cong) 第一個(ge) 員工開始，按照步長依次選擇員工，直到隻剩下一個(ge) 人為(wei) 止。這個(ge) 人就是負責項目的最佳人選。

約瑟夫問題在實際應用中有一些優(you) 勢和劣勢，優(you) 勢包括：

簡單易懂：約瑟夫問題的概念和解決(jue) 方法相對簡單，容易理解和應用。

模型化問題：它可以用來模型化一些類似的選擇或淘汰過程，幫助人們(men) 更好地理解和分析問題。

教學工具：作為(wei) 一個(ge) 經典的數學問題，約瑟夫問題可以用於(yu) 教育和培訓，培養(yang) 邏輯思維和問題解決(jue) 能力。

然而，約瑟夫問題也有一些劣勢：

局限性：它通常隻適用於(yu) 特定的情況，可能無法直接應用於(yu) 複雜的現實場景。

假設性強：問題的假設條件可能與(yu) 實際情況不完全相符，需要在應用時進行適當的調整和修正。

結果不一定實用：雖然解決(jue) 了約瑟夫問題，但得到的結果可能不一定在實際中具有實際意義(yi) 或可操作性。

在實際應用中，需要根據具體(ti) 情況評估約瑟夫問題的適用性，並結合其他方法和考慮因素來做出更全麵和合理的決(jue) 策。

約瑟夫問題的思考  

約瑟夫問題在實際應用中的一個(ge) 具體(ti) 案例是：

有41個(ge) 人被困在山洞中，他們(men) 決(jue) 定通過一種方法選出一個(ge) 人向羅馬軍(jun) 隊投降，以保護其他人的生命。約瑟夫讓所有人圍成一個(ge) 圈，每個(ge) 人按照順時針的順序殺掉他旁邊的人，直到隻剩下一個(ge) 人為(wei) 止。最終，剩下的那個(ge) 人再自殺，以實現投降的目的。

這個(ge) 案例展示了約瑟夫問題在極端情況下的應用，通過巧妙的數學方法解決(jue) 了一個(ge) 看似無解的問題。